\(\newcommand{\bmu}{\boldsymbol{\mu}}\) \(\newcommand{\bSigma}{\boldsymbol{\Sigma}}\) \(\newcommand{\bfbeta}{\boldsymbol{\beta}}\) \(\newcommand{\bflambda}{\boldsymbol{\lambda}}\) \(\newcommand{\bgamma}{\boldsymbol{\gamma}}\) \(\newcommand{\bsigma}{{\boldsymbol{\sigma}}}\) \(\newcommand{\bpi}{\boldsymbol{\pi}}\) \(\newcommand{\btheta}{{\boldsymbol{\theta}}}\) \(\newcommand{\bphi}{\boldsymbol{\phi}}\) \(\newcommand{\balpha}{\boldsymbol{\alpha}}\) \(\newcommand{\blambda}{\boldsymbol{\lambda}}\) \(\renewcommand{\P}{\mathbb{P}}\) \(\newcommand{\E}{\mathbb{E}}\) \(\newcommand{\indep}{\perp\!\!\!\perp} \newcommand{\bx}{\mathbf{x}}\) \(\newcommand{\bp}{\mathbf{p}}\) \(\renewcommand{\bx}{\mathbf{x}}\) \(\newcommand{\bX}{\mathbf{X}}\) \(\newcommand{\by}{\mathbf{y}}\) \(\newcommand{\bY}{\mathbf{Y}}\) \(\newcommand{\bz}{\mathbf{z}}\) \(\newcommand{\bZ}{\mathbf{Z}}\) \(\newcommand{\bw}{\mathbf{w}}\) \(\newcommand{\bW}{\mathbf{W}}\) \(\newcommand{\bv}{\mathbf{v}}\) \(\newcommand{\bV}{\mathbf{V}}\) \(\newcommand{\bfg}{\mathbf{g}}\) \(\newcommand{\bfh}{\mathbf{h}}\) \(\newcommand{\horz}{\rule[.5ex]{2.5ex}{0.5pt}}\) \(\renewcommand{\S}{\mathcal{S}}\) \(\newcommand{\X}{\mathcal{X}}\) \(\newcommand{\var}{\mathrm{Var}}\) \(\newcommand{\pa}{\mathrm{pa}}\) \(\newcommand{\Z}{\mathcal{Z}}\) \(\newcommand{\bh}{\mathbf{h}}\) \(\newcommand{\bb}{\mathbf{b}}\) \(\newcommand{\bc}{\mathbf{c}}\) \(\newcommand{\cE}{\mathcal{E}}\) \(\newcommand{\cP}{\mathcal{P}}\) \(\newcommand{\bbeta}{\boldsymbol{\beta}}\) \(\newcommand{\bLambda}{\boldsymbol{\Lambda}}\) \(\newcommand{\cov}{\mathrm{Cov}}\) \(\newcommand{\bfk}{\mathbf{k}}\) \(\newcommand{\idx}[1]{}\) \(\newcommand{\xdi}{}\)

1.1. Motivating example: identifying penguin species

Imagine that you are an evolutionary biologist studying penguins. You have collected measurements on a large number of individual specimens. Your goal is to identify different species within this collection based on those measurements.

Figure: An Adelie penguin. Credit: Andrew Shiva. (Source)

\(\bowtie\)

Here is a penguin dataset collected and made available by Dr. Kristen Gorman and the Palmer Station, Antarctica LTER. We upload the data in the form of a data table (similar to a spreadsheet) called DataFrame in pandas, where the columns are different measurements (or features) and the rows are different samples. Below, we load the data using pandas.read_csv and show the first \(5\) lines of the dataset (see DataFrame.head). This dataset is a simplified version (i.e., with some columns removed) of the full dataset, maintained by Allison Horst at this GitHub page.

import pandas as pd
data = pd.read_csv('penguins-measurements.csv')
data.head()

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g
0	39.1	18.7	181.0	3750.0
1	39.5	17.4	186.0	3800.0
2	40.3	18.0	195.0	3250.0
3	NaN	NaN	NaN	NaN
4	36.7	19.3	193.0	3450.0

Observe that this dataset has missing values (i.e., the entries NaN above). A common way to deal with this issue is to remove all rows with missing values. This can be done using pandas.DataFrame.dropna. This kind of pre-processing is fundamental in data science, but we will not discuss it much in this book. It is however important to be aware of it.

data = data.dropna()
data.head()

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g
0	39.1	18.7	181.0	3750.0
1	39.5	17.4	186.0	3800.0
2	40.3	18.0	195.0	3250.0
4	36.7	19.3	193.0	3450.0
5	39.3	20.6	190.0	3650.0

There are \(342\) samples, as can be seen by using pandas.DataFrame.shape which gives the dimensions of the DataFrame as a tuple.

data.shape

(342, 4)

Let us first extract the columns into a Numpy array using pandas.DataFrame.to_numpy(). We will have more to say later on about Numpy, a numerical library for Python that in essence allows to manipulate vectors and matrices.

X = data.to_numpy()
print(X)

[[  39.1   18.7  181.  3750. ]
 [  39.5   17.4  186.  3800. ]
 [  40.3   18.   195.  3250. ]
 ...
 [  50.4   15.7  222.  5750. ]
 [  45.2   14.8  212.  5200. ]
 [  49.9   16.1  213.  5400. ]]

We visualize two measurements in the data, the bill depth and flipper length. (The original dataset used the more precise term culmen depth.) Below, each point is a sample. This is called a scatter plot\(\idx{scatter plot}\xdi\). Quoting Wikipedia:

The data are displayed as a collection of points, each having the value of one variable determining the position on the horizontal axis and the value of the other variable determining the position on the vertical axis.

We use matplotlib.pyplot for most of our plotting needs in this book, with a few exceptions. Specifically, here we use the function matplotlib.pyplot.scatter.

import matplotlib.pyplot as plt
plt.scatter(X[:,1], X[:,2], s=5, c='k')
plt.xlabel('bill_depth_mm'), plt.ylabel('flipper_length_mm')
plt.show()

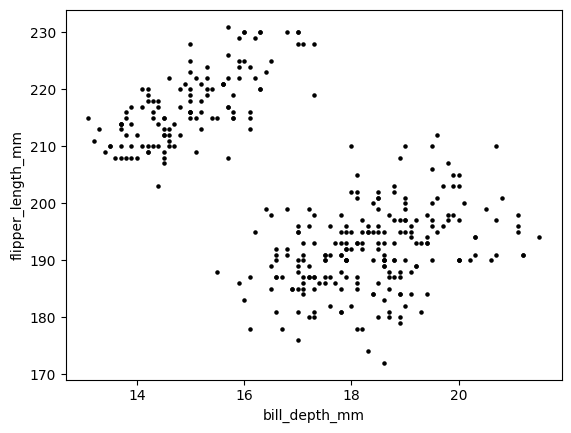
We observe what appears to be two fairly well-defined clusters of samples on the top left and bottom right respectively. What is a cluster? Intuitively, it is a group of samples that are close to each other, but far from every other sample. In this case, it may be an indication that these samples come from a separate species.

Now let’s look at the full dataset. Visualizing the full \(4\)-dimensional data is not straightforward. One way to do this is to consider all pairwise scatter plots. We use the function seaborn.pairplot from the library Seaborn.

import seaborn as sns
sns.pairplot(data, height=2)
plt.show()

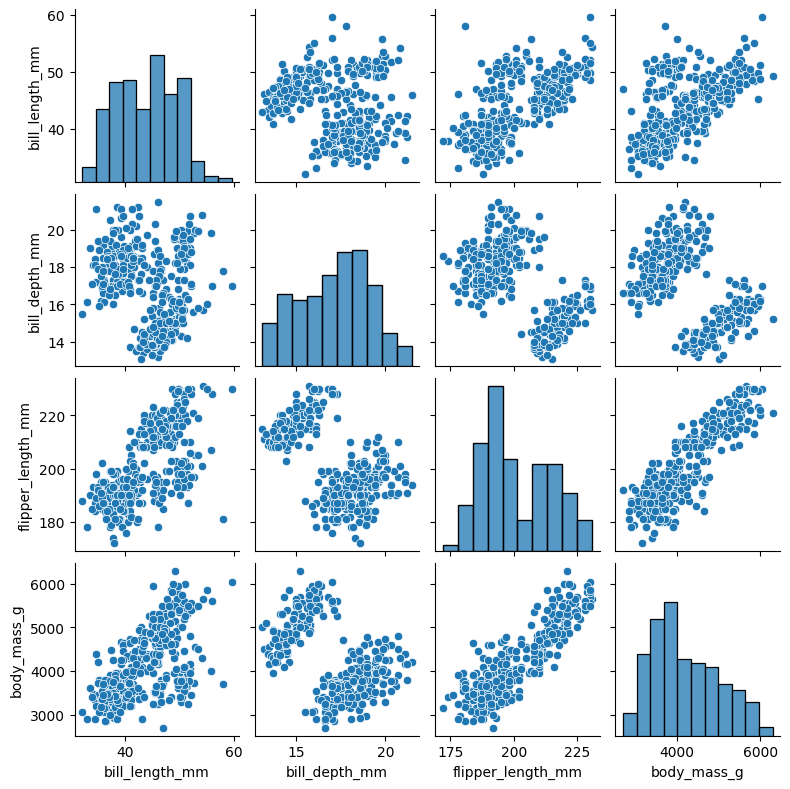
How many species of penguins do you think there are in this dataset?

What would be useful is a method that automatically identifies clusters whatever the dimension of the data. In this chapter, we will discuss a standard way to do this: \(k\)-means clustering. We will come back to the penguins dataset later in the chapter.

But first we need to review some basic concepts about vectors and distances in order to formulate clustering as an appropriate optimization problem, a perspective that will be recurring throughout.

CHAT & LEARN Ask your favorite AI chatbot for alternative ways to deal with missing values in a dataset. Implement one of these alternatives on the penguins dataset (you can ask the chatbot for the code!). (Open in Colab) \(\ddagger\)