Geometry of least squares: the orthogonal projection

$\newcommand{\bmu}{\boldsymbol{\mu}}$ $\newcommand{\bSigma}{\boldsymbol{\Sigma}}$ $\newcommand{\bfbeta}{\boldsymbol{\beta}}$ $\newcommand{\bflambda}{\boldsymbol{\lambda}}$ $\newcommand{\bgamma}{\boldsymbol{\gamma}}$ $\newcommand{\bsigma}{{\boldsymbol{\sigma}}}$ $\newcommand{\bpi}{\boldsymbol{\pi}}$ $\newcommand{\btheta}{{\boldsymbol{\theta}}}$ $\newcommand{\bphi}{\boldsymbol{\phi}}$ $\newcommand{\balpha}{\boldsymbol{\alpha}}$ $\newcommand{\blambda}{\boldsymbol{\lambda}}$ $\renewcommand{\P}{\mathbb{P}}$ $\newcommand{\E}{\mathbb{E}}$ $\newcommand{\indep}{\perp\!\!\!\perp} \newcommand{\bx}{\mathbf{x}}$ $\newcommand{\bp}{\mathbf{p}}$ $\renewcommand{\bx}{\mathbf{x}}$ $\newcommand{\bX}{\mathbf{X}}$ $\newcommand{\by}{\mathbf{y}}$ $\newcommand{\bY}{\mathbf{Y}}$ $\newcommand{\bz}{\mathbf{z}}$ $\newcommand{\bZ}{\mathbf{Z}}$ $\newcommand{\bw}{\mathbf{w}}$ $\newcommand{\bW}{\mathbf{W}}$ $\newcommand{\bv}{\mathbf{v}}$ $\newcommand{\bV}{\mathbf{V}}$ $\newcommand{\bfg}{\mathbf{g}}$ $\newcommand{\bfh}{\mathbf{h}}$ $\newcommand{\horz}{\rule[.5ex]{2.5ex}{0.5pt}}$ $\renewcommand{\S}{\mathcal{S}}$ $\newcommand{\X}{\mathcal{X}}$ $\newcommand{\var}{\mathrm{Var}}$ $\newcommand{\pa}{\mathrm{pa}}$ $\newcommand{\Z}{\mathcal{Z}}$ $\newcommand{\bh}{\mathbf{h}}$ $\newcommand{\bb}{\mathbf{b}}$ $\newcommand{\bc}{\mathbf{c}}$ $\newcommand{\cE}{\mathcal{E}}$ $\newcommand{\cP}{\mathcal{P}}$ $\newcommand{\bbeta}{\boldsymbol{\beta}}$ $\newcommand{\bLambda}{\boldsymbol{\Lambda}}$ $\newcommand{\cov}{\mathrm{Cov}}$ $\newcommand{\bfk}{\mathbf{k}}$ $\newcommand{\idx}[1]{}$ $\newcommand{\xdi}{}$

2.3. Geometry of least squares: the orthogonal projection#

We consider the following problem: we are given $A \in \mathbb{R}^{n\times m}$ an $n\times m$ matrix and $\mathbf{b} \in \mathbb{R}^n$ a vector. We are looking to solve the system $A \mathbf{x} \approx \mathbf{b}$. In the special case where $A$ is invertible, a unique exact solution exists. In general, however, a solution may not exist or may not be unique. We focus here on the over-determined case where the former situation generically occurs. We begin by rewieving the concept of orthogonality.

2.3.1. A key concept: orthogonality#

Orthogonality plays a key role in linear algebra for data science thanks to its computational properties and its connection to the least-squares problem.

DEFINITION (Orthogonality) $\idx{orthogonality}\xdi$ Vectors $\mathbf{u}$ and $\mathbf{v}$ in $\mathbb{R}^n$ (as column vectors) are orthogonal if their inner product is zero

\[ \langle \mathbf{u}, \mathbf{v} \rangle =\mathbf{u}^T \mathbf{v} = \sum_{i=1}^n u_i v_i = 0. \]

$\natural$

Orthogonality has important implications. The following classical result will be useful below. Throughout, we use $\|\mathbf{u}\|$ for the Euclidean norm of $\mathbf{u}$.

THEOREM (Pythagoras) $\idx{Pythagoras' theorem}\xdi$ Let $\mathbf{u}, \mathbf{v} \in \mathbb{R}^n$ be orthogonal. Then $\|\mathbf{u} + \mathbf{v}\|^2 = \|\mathbf{u}\|^2 + \|\mathbf{v}\|^2$. $\sharp$

Proof: Using $\|\mathbf{w}\|^2 = \langle \mathbf{w}, \mathbf{w}\rangle$, we get

\[\begin{align*} \|\mathbf{u} + \mathbf{v}\|^2 &= \langle \mathbf{u} + \mathbf{v}, \mathbf{u} + \mathbf{v}\rangle\\ &= \langle \mathbf{u}, \mathbf{u}\rangle + 2 \,\langle \mathbf{u}, \mathbf{v}\rangle + \langle \mathbf{v}, \mathbf{v}\rangle\\ &= \|\mathbf{u}\|^2 + \|\mathbf{v}\|^2. \end{align*}\]

$\square$

An application of Pythagoras’ Theorem is a proof of the Cauchy-Schwarz Inequality.

Proof: (Cauchy-Schwarz) $\idx{Cauchy-Schwarz inequality}\xdi$ Let $\mathbf{q} = \frac{\mathbf{v}}{\|\mathbf{v}\|}$ be the unit vector in the direction of $\mathbf{v}$. We want to show $|\langle \mathbf{u}, \mathbf{q}\rangle| \leq \|\mathbf{u}\|$. Decompose $\mathbf{u}$ as follows:

\[ \mathbf{u} = \left\langle \mathbf{u}, \mathbf{q}\right\rangle \mathbf{q} + \left\{\mathbf{u} - \left\langle \mathbf{u}, \mathbf{q}\right\rangle \mathbf{q}\right\}. \]

The two terms on the right-hand side are orthogonal:

\[ \left\langle \left\langle \mathbf{u}, \mathbf{q}\right\rangle \mathbf{q}, \mathbf{u} - \left\langle \mathbf{u}, \mathbf{q}\right\rangle \mathbf{q} \right\rangle = \left\langle \mathbf{u}, \mathbf{q}\right\rangle^2 - \left\langle \mathbf{u}, \mathbf{q}\right\rangle^2 \left\langle \mathbf{q}, \mathbf{q}\right\rangle = 0. \]

So Pythagoras gives

\[ \|\mathbf{u}\|^2 = \left\|\left\langle \mathbf{u}, \mathbf{q}\right\rangle \mathbf{q}\right\|^2 + \left\|\mathbf{u} - \left\langle \mathbf{u}, \mathbf{q}\right\rangle \mathbf{q}\right\|^2 \geq \left\|\left\langle \mathbf{u}, \mathbf{q}\right\rangle \mathbf{q}\right\|^2 = \left\langle \mathbf{u}, \mathbf{q}\right\rangle^2. \]

Taking a square root gives the claim. $\square$

Orthonormal basis expansion To begin to see the power of orthogonality, consider the following. A list of vectors $\{\mathbf{u}_1,\ldots,\mathbf{u}_m\}$ is an orthonormal list if the $\mathbf{u}_i$’s are pairwise orthogonal and each has norm 1, that is, for all $i$ and all $j \neq i$, we have $\|\mathbf{u}_i\| = 1$ and $\langle \mathbf{u}_i, \mathbf{u}_j \rangle = 0$. Alternatively,

\[\begin{split} \langle \mathbf{u}_i, \mathbf{u}_j \rangle = \begin{cases} 1 & \text{if $i=j$}\\ 0 & \text{if $i\neq j$}. \end{cases} \end{split}\]

LEMMA (Properties of Orthonormal Lists) $\idx{properties of orthonormal lists}\xdi$ Let $\{\mathbf{u}_1,\ldots,\mathbf{u}_m\}$ be an orthonormal list. Then:

for any $\alpha_j \in \mathbb{R}$, $j=1,\ldots,m$, we have

\[ \left\|\sum_{j=1}^m \alpha_j \mathbf{u}_j\right\|^2 = \sum_{j=1}^m \alpha_j^2, \]

the vectors $\{\mathbf{u}_1,\ldots,\mathbf{u}_m\}$ are linearly independent.

$\flat$

Proof: For 1., using that $\|\mathbf{x}\|^2 = \langle \mathbf{x}, \mathbf{x} \rangle$, we have

\[\begin{align*} \left\|\sum_{j=1}^m \alpha_j \mathbf{u}_j\right\|^2 &= \left\langle \sum_{i=1}^m \alpha_i \mathbf{u}_i, \sum_{j=1}^m \alpha_j \mathbf{u}_j \right\rangle\\ &= \sum_{i=1}^m \alpha_i \left\langle \mathbf{u}_i, \sum_{j=1}^m \alpha_j \mathbf{u}_j \right\rangle\\ &= \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j \left\langle \mathbf{u}_i, \mathbf{u}_j \right\rangle\\ &= \sum_{i=1}^m \alpha_i^2 \end{align*}\]

where we used orthonormality in the last equation, that is, $\langle \mathbf{u}_i, \mathbf{u}_j \rangle$ is $1$ if $i=j$ and $0$ otherwise.

For 2., suppose $\sum_{i=1}^m \beta_i \mathbf{u}_i = \mathbf{0}$, then we must have by 1. that $\sum_{i=1}^m \beta_i^2 = 0$. That implies $\beta_i = 0$ for all $i$. Hence the $\mathbf{u}_i$’s are linearly independent. $\square$

Given a basis $\{\mathbf{u}_1,\ldots,\mathbf{u}_m\}$ of $U$, we know that: for any $\mathbf{w} \in U$, $\mathbf{w} = \sum_{i=1}^m \alpha_i \mathbf{u}_i$ for some $\alpha_i$’s. It is not immediately obvious in general how to find the $\alpha_i$’s. In the orthonormal case, however, there is a formula. We say that the basis $\{\mathbf{u}_1,\ldots,\mathbf{u}_m\}$ is orthonormal if it forms an orthonormal list.

THEOREM (Orthonormal Expansion) $\idx{orthonormal expansion theorem}\xdi$ Let $\mathbf{q}_1,\ldots,\mathbf{q}_m$ be an orthonormal basis of $U$ and let $\mathbf{w} \in U$. Then

\[ \mathbf{w} = \sum_{j=1}^m \langle \mathbf{w}, \mathbf{q}_j\rangle \,\mathbf{q}_j. \]

$\sharp$

Proof: Because $\mathbf{w} \in U$, $\mathbf{w} = \sum_{i=1}^m \alpha_i \mathbf{q}_i$ for some $\alpha_i$. Take the inner product with $\mathbf{q}_j$ and use orthonormality:

\[ \langle \mathbf{w}, \mathbf{q}_j\rangle = \left\langle \sum_{i=1}^m \alpha_i \mathbf{q}_i, \mathbf{q}_j\right\rangle = \sum_{i=1}^m \alpha_i \langle \mathbf{q}_i, \mathbf{q}_j\rangle = \alpha_j. \]

Hence, we have determined all $\alpha_j$’s in the basis expansion of $\mathbf{w}$. $\square$

EXAMPLE: Consider again the linear subspace $W = \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2,\mathbf{w}_3)$, where $\mathbf{w}_1 = (1,0,1)$, $\mathbf{w}_2 = (0,1,1)$, and $\mathbf{w}_3 = (1,-1,0)$. We have shown that in fact

\[ \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2,\mathbf{w}_3) = \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2). \]

as $\mathbf{w}_1,\mathbf{w}_2$ form a basis of $W$. On the other hand,

\[ \langle\mathbf{w}_1,\mathbf{w}_2\rangle = (1)(0) + (0)(1) + (1)(1) = 0 + 0 + 1 = 1 \neq 0 \]

so this basis is not orthonormal. Indeed, an orthonormal list is necessarily an independent list, but the opposite may not hold.

To produce an orthonormal basis of $W$, we can first proceed by normalizing $\mathbf{w}_1$

\[ \mathbf{q}_1 = \frac{\mathbf{w}_1}{\|\mathbf{w}_1\|} = \frac{\mathbf{w}_1}{\sqrt{1^2 + 0^2 + 1^2}} = \frac{1}{\sqrt{2}} \mathbf{w}_1. \]

Then $\|\mathbf{q}_1\| = 1$ since, in general, by homogeneity of the norm

\[ \left\|\frac{\mathbf{w}_1}{\|\mathbf{w}_1\|}\right\| = \frac{1}{\|\mathbf{w}_1\|} \|\mathbf{w}_1\| = 1. \]

We then seek a second basis vector. It must satisfy two conditions in this case:

it must be of unit norm and be orthogonal to $\mathbf{q}_1$; and
$\mathbf{w}_2$ must be a linear combination of $\mathbf{q}_1$ and $\mathbf{q}_2$.

The latter condition guarantees that $\mathrm{span}(\mathbf{q}_1,\mathbf{q}_2) = \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2)$. (Formally, that would imply only that $\mathrm{span}(\mathbf{w}_1,\mathbf{w}_2) \subseteq \mathrm{span}(\mathbf{q}_1,\mathbf{q}_2)$. In this case, it is easy to see that the containment must go in the opposite direction as well. Why?)

The first condition translates into

\[ 1 = \|\mathbf{q}_2\|^2 = q_{21}^2 + q_{22}^2 + q_{23}^2, \]

where $\mathbf{q}_2 = (q_{21}, q_{22}, q_{23})$, and

\[ 0 = \langle\mathbf{q}_1, \mathbf{q}_2\rangle = \frac{1}{\sqrt{2}}\left[1\cdot q_{21} + 0 \cdot q_{22} + 1 \cdot q_{23}\right] = \frac{1}{\sqrt{2}}\left[q_{21} + q_{23}\right]. \]

That is, simplifying the second display and plugging into the first, $q_{23} = -q_{21}$ and $q_{22} = \sqrt{1 - 2 q_{21}^2}$.

The second condition translates into: there is $\beta_1, \beta_2 \in \mathbb{R}$ such that

\[\begin{split} \mathbf{w}_2 = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \beta_1 \mathbf{q}_1 + \beta_2 \mathbf{q}_2 = \beta_1 \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + \beta_2 \begin{pmatrix} q_{21} \\ \sqrt{1-2 q_{21}^2} \\ -q_{21} \end{pmatrix}. \end{split}\]

The first entry gives $\beta_1/\sqrt{2} + \beta_2 q_{21} = 0$ while the third entry gives $\beta_1/\sqrt{2} - \beta_2 q_{21} = 1$. Adding up the equations gives $\beta_1 = 1/\sqrt{2}$. Plugging back into the first one gives $\beta_2 = -1/(2q_{21})$. Returning to the equation for $\mathbf{w}_2$, we get from the second entry

\[ 1 = - \frac{1}{2 q_{21}} \sqrt{1 - 2 q_{21}^2}. \]

Rearranging and taking a square, we want the negative solution to

\[ 4 q_{21}^2 = 1 - 2 q_{21}^2, \]

that is, $q_{21} = - 1/\sqrt{6}$. Finally, we get $q_{23} = - q_{21} = 1/\sqrt{6}$ and $q_{22} = \sqrt{1 - 2 q_{21}^2} = \sqrt{1 - 1/3} = \sqrt{2/3} = 2/\sqrt{6}$.

To summarize, we have

\[\begin{split} \mathbf{q}_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix}, \quad \mathbf{q}_2 = \frac{1}{\sqrt{6}} \begin{pmatrix} -1\\ 2\\ 1 \end{pmatrix}. \end{split}\]

We confirm that

\[ \langle \mathbf{q}_1, \mathbf{q}_2\rangle = \frac{1}{\sqrt{2}\sqrt{6}}[(1)(-1) + (0)(2) + (1)(1)] = 0 \]

and

\[ \|\mathbf{q}_2\|^2 = \left(-\frac{1}{\sqrt{6}}\right)^2 + \left(\frac{2}{\sqrt{6}}\right)^2 + \left(\frac{1}{\sqrt{6}}\right)^2 = \frac{1}{6} + \frac{4}{6} + \frac{1}{6} = 1. \]

We can use the Orthonormal Expansion Theorem to write $\mathbf{w}_2$ as a linear combination of $\mathbf{q}_1$ and $\mathbf{q}_2$. The inner products are

\[ \langle \mathbf{w}_2, \mathbf{q}_1 \rangle = 0 \left(\frac{1}{\sqrt{2}}\right) + 1 \left(\frac{0}{\sqrt{2}}\right) + 1 \left(\frac{1}{\sqrt{2}}\right) = \frac{1}{\sqrt{2}}, \]

\[ \langle \mathbf{w}_2, \mathbf{q}_2 \rangle = 0 \left(-\frac{1}{\sqrt{6}}\right) + 1 \left(\frac{2}{\sqrt{6}}\right) + 1 \left(\frac{1}{\sqrt{6}}\right) = \frac{3}{\sqrt{6}}. \]

So

\[ \mathbf{w}_2 = \frac{1}{\sqrt{2}} \mathbf{q}_1 + \frac{3}{\sqrt{6}} \mathbf{q}_2. \]

Check it! Try $\mathbf{w}_3$. $\lhd$

Gram-Schmidt We have shown that working with orthonormal bases is desirable. What if we do not have one? We could try to construct one by hand as we did in the previous example. But there are better ways. We review the Gram-Schmidt algorithm in an upcoming section, which will imply that every linear subspace has an orthonormal basis. That is, we will prove the following theorem.

THEOREM (Gram-Schmidt) $\idx{Gram-Schmidt theorem}\xdi$ Let $\mathbf{a}_1,\ldots,\mathbf{a}_m$ be linearly independent. Then there exists an orthonormal basis $\mathbf{q}_1,\ldots,\mathbf{q}_m$ of $\mathrm{span}(\mathbf{a}_1,\ldots,\mathbf{a}_m)$. $\sharp$

But, first, we will need to define the orthogonal projection, which will play a key role in our applications. This is done in the next section.

2.3.2. Orthogonal projection#

To solve the overdetermined case, i.e., when $n > m$, we consider the following more general problem first. We have a linear subspace $U \subseteq \mathbb{R}^n$ and a vector $\mathbf{v} \notin U$. We want to find the vector $\mathbf{p}$ in $U$ that is closest to $\mathbf{v}$ in Euclidean norm, that is, we want to solve

\[ \min_{\mathbf{p} \in U} \|\mathbf{p} - \mathbf{v}\|. \]

EXAMPLE: Consider the two-dimensional case with a one-dimensional subspace, say $U = \mathrm{span}(\mathbf{u_1})$ with $\|\mathbf{u}_1\|=1$. The geometrical intuition is in the following figure. The solution $\mathbf{p} = \mathbf{v}^*$ has the property that the difference $\mathbf{v} - \mathbf{v}^*$ makes a right angle with $\mathbf{u}_1$, that is, it is orthogonal to it.

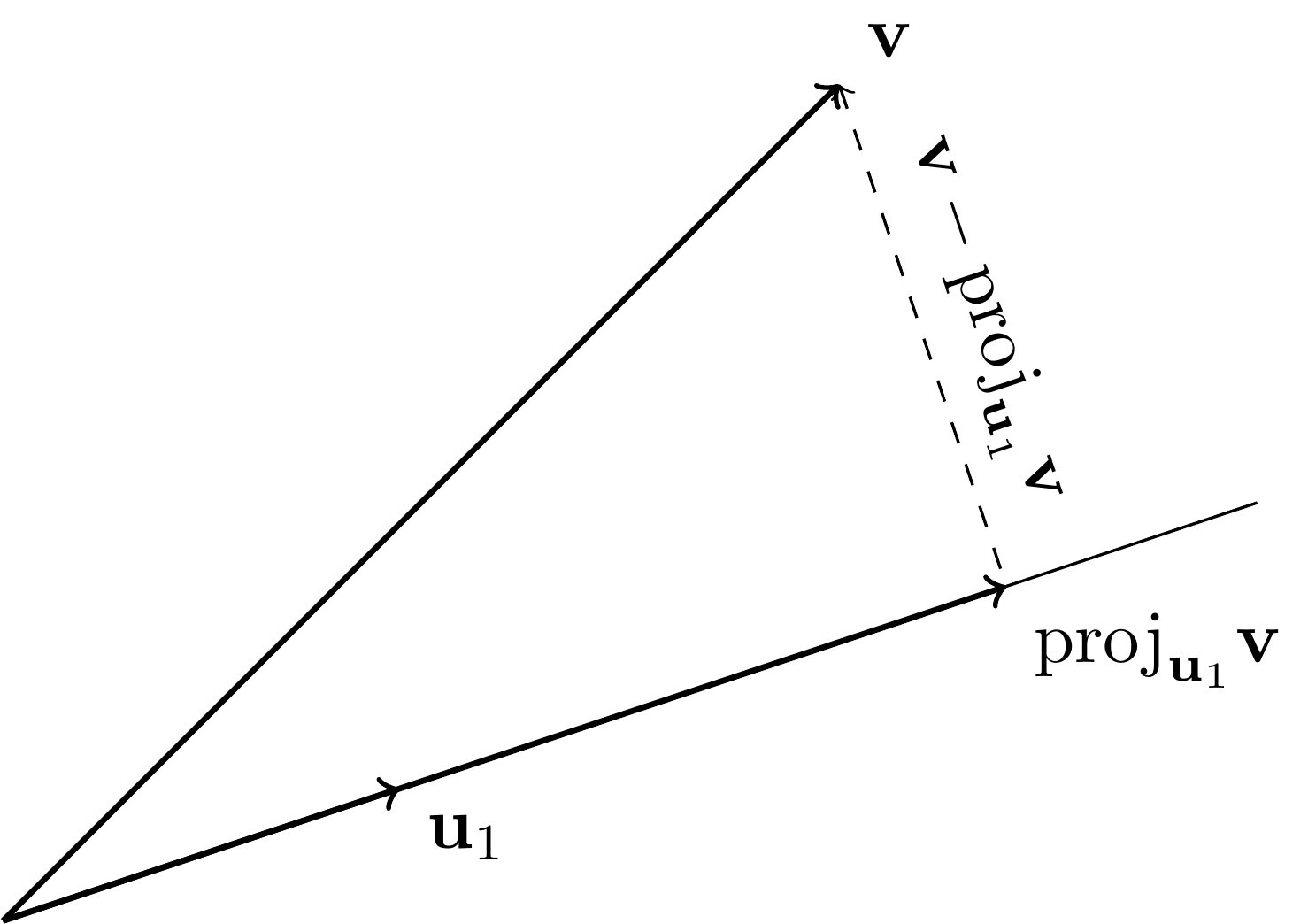
Letting $\mathbf{v}^* = \alpha^* \,\mathbf{u}_1$, the geometrical condition above translates into

\[ 0 = \langle \mathbf{u}_1, \mathbf{v} - \mathbf{v}^* \rangle = \langle \mathbf{u}_1, \mathbf{v} - \alpha^* \,\mathbf{u}_1 \rangle = \langle \mathbf{u}_1, \mathbf{v} \rangle - \alpha^* \,\langle \mathbf{u}_1, \mathbf{u}_1 \rangle = \langle \mathbf{u}_1, \mathbf{v} \rangle - \alpha^* \]

so

\[ \mathbf{v}^* = \langle \mathbf{u}_1, \mathbf{v} \rangle \,\mathbf{u}_1. \]

By Pythagoras’ Theorem, we then have for any $\alpha \in \mathbb{R}$

\[\begin{align*} \|\mathbf{v} - \alpha \,\mathbf{u}_1\|^2 &= \|\mathbf{v}- \mathbf{v}^* + \mathbf{v}^* - \alpha \,\mathbf{u}_1\|^2\\ &= \|\mathbf{v}- \mathbf{v}^* + (\alpha^* - \alpha) \,\mathbf{u}_1\|^2\\ &= \|\mathbf{v}- \mathbf{v}^*\|^2 + \| (\alpha^* - \alpha) \,\mathbf{u}_1\|^2\\ &\geq \|\mathbf{v}- \mathbf{v}^*\|^2, \end{align*}\]

where we used that $\mathbf{v} - \mathbf{v}^*$ is orthogonal to $\mathbf{u}_1$ (and therefore $(\alpha^* - \alpha) \mathbf{u}_1$) on the third line.

That confirms the optimality of $\mathbf{v}^*$. The argument in this example carries through in higher dimension, as we show next. $\lhd$

DEFINITION (Orthogonal Projection on an Orthonormal List) $\idx{orthogonal projection on an orthonormal list}\xdi$ Let $\mathbf{q}_1,\ldots,\mathbf{q}_m$ be an orthonormal list. The orthogonal projection of $\mathbf{v} \in \mathbb{R}^n$ on $\{\mathbf{q}_i\}_{i=1}^m$ is defined as

\[ \mathrm{proj}_{\{\mathbf{q}_i\}_{i=1}^m} \mathbf{v} = \sum_{j=1}^m \langle \mathbf{v}, \mathbf{q}_j \rangle \,\mathbf{q}_j. \]

$\natural$

THEOREM (Orthogonal Projection) $\idx{orthogonal projection theorem}\xdi$ Let $U \subseteq V$ be a linear subspace and let $\mathbf{v} \in \mathbb{R}^n$. Then:

a) There exists a unique solution $\mathbf{p}^*$ to

\[ \min_{\mathbf{p} \in U} \|\mathbf{p} - \mathbf{v}\|. \]

We denote it by $\mathbf{p}^* = \mathrm{proj}_U \mathbf{v}$ and refer to it as the orthogonal projection of $\mathbf{v}$ onto $U$.

b) The solution $\mathbf{p}^*$ is characterized geometrically by

\[ (*) \qquad \left\langle \mathbf{v} - \mathbf{p}^*, \mathbf{u}\right\rangle =0, \quad \forall \mathbf{u} \in U. \]

c) For any orthonormal basis $\mathbf{q}_1,\ldots,\mathbf{q}_m$ of $U$,

\[ \mathrm{proj}_U \mathbf{v} = \mathrm{proj}_{\{\mathbf{q}_i\}_{i=1}^m} \mathbf{v}. \]

$\sharp$

Proof: Let $\mathbf{p}^*$ be any vector in $U$ satisfying $(*)$. We show first that it necessarily satisfies

\[ (**) \qquad \|\mathbf{p}^* - \mathbf{v}\| \leq \|\mathbf{p} - \mathbf{v}\|, \quad \forall \mathbf{p} \in U. \]

Note that for any $\mathbf{p} \in U$ the vector $\mathbf{u} = \mathbf{p} - \mathbf{p}^*$ is also in $U$. Hence by $(*)$ and Pythagoras,

\[\begin{align*} \|\mathbf{p} - \mathbf{v}\|^2 &= \|\mathbf{p} - \mathbf{p}^* + \mathbf{p}^* - \mathbf{v}\|^2\\ &= \|\mathbf{p} - \mathbf{p}^*\|^2 + \|\mathbf{p}^* - \mathbf{v}\|^2\\ &\geq \|\mathbf{p}^* - \mathbf{v}\|^2. \end{align*}\]

Furthermore, equality holds only if $\|\mathbf{p} - \mathbf{p}^*\|^2 = 0$ which holds only if $\mathbf{p} = \mathbf{p}^*$ by the point-separating property of the Euclidean norm. Hence, if such a vector $\mathbf{p}^*$ exists, it is unique.

It remains to show that there is at least one vector in $U$ satisfying $(*)$. By the Gram-Schmidt Theorem, the linear subspace $U$ has an orthonormal basis $\mathbf{q}_1,\ldots,\mathbf{q}_m$. By definition, $\mathrm{proj}_{\{\mathbf{q}_i\}_{i=1}^m} \mathbf{v} \in \mathrm{span}(\{\mathbf{q}_i\}_{i=1}^m) = U$. We show that $\mathrm{proj}_{\{\mathbf{q}_i\}_{i=1}^m} \mathbf{v}$ satisfies $(*)$. We can write any $\mathbf{u} \in U$ as $\sum_{i=1}^m \alpha_i \mathbf{q}_i$ with $\alpha_i = \langle \mathbf{u}, \mathbf{q}_i \rangle$. So, using this representation, we get

\[\begin{align*} \left\langle \mathbf{v} - \sum_{j=1}^m \langle \mathbf{v}, \mathbf{q}_j \rangle \,\mathbf{q}_j, \sum_{i=1}^m \alpha_i \mathbf{q}_i \right\rangle &= \sum_{j=1}^m \langle \mathbf{v}, \mathbf{q}_j \rangle \,\alpha_j - \sum_{j=1}^m \sum_{i=1}^m \alpha_i \langle \mathbf{v}, \mathbf{q}_j \rangle \langle \mathbf{q}_j, \mathbf{q}_i \rangle\\ &= \sum_{j=1}^m \langle \mathbf{v}, \mathbf{q}_j \rangle \,\alpha_j - \sum_{j=1}^m \alpha_j \langle \mathbf{v}, \mathbf{q}_j \rangle\\ &= 0, \end{align*}\]

where we used the orthonormality of the $\mathbf{q}_j$’s on the second line. $\square$

EXAMPLE: (continued) Consider again the linear subspace $W = \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2,\mathbf{w}_3)$, where $\mathbf{w}_1 = (1,0,1)$, $\mathbf{w}_2 = (0,1,1)$, and $\mathbf{w}_3 = (1,-1,0)$. We have shown that

\[\begin{split} \mathbf{q}_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix}, \quad \mathbf{q}_2 = \frac{1}{\sqrt{6}} \begin{pmatrix} -1\\ 2\\ 1 \end{pmatrix}, \end{split}\]

is an orthonormal basis. Let $\mathbf{w}_4 = (0,0,2)$. It is immediate that $\mathbf{w}_4 \notin \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2)$ since vectors in that span are of the form $(x,y,x+y)$ for some $x,y \in \mathbb{R}$.

We can however compute the orthogonal projection $\mathbf{w}_4$ onto $W$. The inner products are

\[ \langle \mathbf{w}_4, \mathbf{q}_1 \rangle = 0 \left(\frac{1}{\sqrt{2}}\right) + 0 \left(\frac{0}{\sqrt{2}}\right) + 2 \left(\frac{1}{\sqrt{2}}\right) = \frac{2}{\sqrt{2}}, \]

\[ \langle \mathbf{w}_4, \mathbf{q}_2 \rangle = 0 \left(-\frac{1}{\sqrt{6}}\right) + 0 \left(\frac{2}{\sqrt{6}}\right) + 2 \left(\frac{1}{\sqrt{6}}\right) = \frac{2}{\sqrt{6}}. \]

So

\[\begin{split} \mathrm{proj}_W \mathbf{w}_4 = \frac{2}{\sqrt{2}} \mathbf{q}_1 + \frac{2}{\sqrt{6}} \mathbf{q}_2 = \begin{pmatrix} 2/3\\ 2/3\\ 4/3 \end{pmatrix}. \end{split}\]

As a sanity check, note that $\mathbf{w}_4 \in W$ since its third entry is equal to the sum of its first two entries. $\lhd$

The map $\mathrm{proj}_U$ is linear, that is, $\mathrm{proj}_U (\alpha \,\mathbf{x} + \mathbf{y}) = \alpha \,\mathrm{proj}_U \mathbf{x} + \mathrm{proj}_U\mathbf{y}$ for all $\alpha \in \mathbb{R}$ and $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$. Indeed,

\[\begin{align*} \mathrm{proj}_U(\alpha \,\mathbf{x} + \mathbf{y}) &= \sum_{j=1}^m \langle \alpha \,\mathbf{x} + \mathbf{y}, \mathbf{q}_j \rangle \,\mathbf{q}_j\\ &= \sum_{j=1}^m \left\{\alpha \, \langle \mathbf{x}, \mathbf{q}_j \rangle + \langle \mathbf{y}, \mathbf{q}_j \rangle\right\} \mathbf{q}_j\\ &= \alpha \,\mathrm{proj}_U \mathbf{x} + \mathrm{proj}_U \mathbf{y}. \end{align*}\]

Any linear map from $\mathbb{R}^n$ to $\mathbb{R}^n$ can be encoded as an $n \times n$ matrix $P$.

Let

\[\begin{split} Q = \begin{pmatrix} | & & | \\ \mathbf{q}_1 & \ldots & \mathbf{q}_m \\ | & & | \end{pmatrix} \end{split}\]

and note that computing

\[\begin{split} Q^T \mathbf{v} = \begin{pmatrix} \langle \mathbf{v}, \mathbf{q}_1 \rangle \\ \cdots \\ \langle \mathbf{v}, \mathbf{q}_m \rangle \end{pmatrix} \end{split}\]

lists the coefficients in the expansion of $\mathrm{proj}_U \mathbf{v}$ over the basis $\mathbf{q}_1,\ldots,\mathbf{q}_m$.

Hence we see that

\[ P = Q Q^T. \]

Indeed, for any vector $\mathbf{v}$,

\[ P \mathbf{v} = Q Q^T \mathbf{v} = Q [Q^T \mathbf{v}]. \]

So the output is a linear combination of the columns of $Q$ (i.e., the $\mathbf{q}_i$’s) where the coefficients are the entries of the vector in square brackets $Q^T \mathbf{v}$.

EXAMPLE: (continued) Consider again the linear subspace $W = \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2,\mathbf{w}_3)$, where $\mathbf{w}_1 = (1,0,1)$, $\mathbf{w}_2 = (0,1,1)$, and $\mathbf{w}_3 = (1,-1,0)$, with orthonormal basis

\[\begin{split} \mathbf{q}_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix}, \quad \mathbf{q}_2 = \frac{1}{\sqrt{6}} \begin{pmatrix} -1\\ 2\\ 1 \end{pmatrix}. \end{split}\]

Then orthogonal projection onto $W$ can be written in matrix form as follows. The matrix $Q$ is

\[\begin{split} Q = \begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{6}\\ 0 & 2/\sqrt{6}\\ 1/\sqrt{2} & 1/\sqrt{6} \end{pmatrix}. \end{split}\]

Then

\[\begin{align*} Q Q^T &= \begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{6}\\ 0 & 2/\sqrt{6}\\ 1/\sqrt{2} & 1/\sqrt{6} \end{pmatrix} \begin{pmatrix} 1/\sqrt{2} & 0 & 1/\sqrt{2}\\ -1/\sqrt{6} & 2/\sqrt{6} & 1/\sqrt{6} \end{pmatrix}\\ &= \begin{pmatrix} 2/3 & -1/3 & 1/3\\ -1/3 & 2/3 & 1/3\\ 1/3 & 1/3 & 2/3 \end{pmatrix}. \end{align*}\]

So the projection of $\mathbf{w}_4 = (0,0,2)$ is

\[\begin{split} \begin{pmatrix} 2/3 & -1/3 & 1/3\\ -1/3 & 2/3 & 1/3\\ 1/3 & 1/3 & 2/3 \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 2 \end{pmatrix} = \begin{pmatrix} 2/3\\ 2/3\\ 4/3 \end{pmatrix}, \end{split}\]

as previously computed. $\lhd$

The matrix $P= Q Q^T$ is not to be confused with

\[\begin{split} Q^T Q = \begin{pmatrix} \langle \mathbf{q}_1, \mathbf{q}_1 \rangle & \cdots & \langle \mathbf{q}_1, \mathbf{q}_m \rangle \\ \langle \mathbf{q}_2, \mathbf{q}_1 \rangle & \cdots & \langle \mathbf{q}_2, \mathbf{q}_m \rangle \\ \vdots & \ddots & \vdots \\ \langle \mathbf{q}_m, \mathbf{q}_1 \rangle & \cdots & \langle \mathbf{q}_m, \mathbf{q}_m \rangle \end{pmatrix} = I_{m \times m} \end{split}\]

where $I_{m \times m}$ denotes the $m \times m$ identity matrix.

EXAMPLE: Let $\mathbf{q}_1,\ldots,\mathbf{q}_n$ be an orthonormal basis of $\mathbb{R}^n$ and form the matrix

\[\begin{split} Q = \begin{pmatrix} | & & | \\ \mathbf{q}_1 & \ldots & \mathbf{q}_n \\ | & & | \end{pmatrix}. \end{split}\]

We show that $Q^{-1} = Q^T$.

By the definition of matrix multiplication, recall that

\[\begin{split} Q^T Q = \begin{pmatrix} \langle \mathbf{q}_1, \mathbf{q}_1 \rangle & \cdots & \langle \mathbf{q}_1, \mathbf{q}_n \rangle \\ \langle \mathbf{q}_2, \mathbf{q}_1 \rangle & \cdots & \langle \mathbf{q}_2, \mathbf{q}_n \rangle \\ \vdots & \ddots & \vdots \\ \langle \mathbf{q}_n, \mathbf{q}_1 \rangle & \cdots & \langle \mathbf{q}_n, \mathbf{q}_n \rangle \end{pmatrix} = I_{n \times n} \end{split}\]

where $I_{n \times n}$ denotes the $n \times n$ identity matrix. This of course follows from the fact that the $\mathbf{q}_i$’s are orthonormal.

In the other direction, we claim that $Q Q^T = I_{n \times n}$ as well. Indeed the matrix $Q Q^T$ is the orthogonal projection on the span of the $\mathbf{q}_i$’s, that is, $\mathbb{R}^n$. By the Orthogonal Projection Theorem, the orthogonal projection $Q Q^T \mathbf{v}$ finds the closest vector to $\mathbf{v}$ in the span of the $\mathbf{q}_i$’s. But that span contains all vectors, including $\mathbf{v}$, so we must have $Q Q^T \mathbf{v} = \mathbf{v}$. Since this holds for all $\mathbf{v} \in \mathbb{R}^n$, the matrix $Q Q^T$ is the identity map and we have proved the claim. $\lhd$

Matrices that satisfy

\[ Q^T Q = Q Q^T = I_{n \times n} \]

are called orthogonal matrices.

DEFINITION (Orthogonal Matrix) $\idx{orthogonal matrix}\xdi$ A square matrix $Q \in \mathbb{R}^{m\times m}$ is orthogonal if $Q^T Q = Q Q^T = I_{m \times m}$. $\natural$

KNOWLEDGE CHECK: Let $\mathcal{Z}$ be a linear subspace of $\mathbb{R}^n$ and let $\mathbf{v} \in \mathbb{R}^n$. Show that

\[ \|\mathrm{proj}_{\mathcal{Z}}\mathbf{v}\|_2 \leq \|\mathbf{v}\|_2. \]

[Hint: Use the geometric characterization.] $\checkmark$

2.3.3. Orthogonal complement#

Before returning to overdetermined systems, we take a little detour to derive a consequence of the orthogonal projection that will be useful later. The Orthogonal Projection Theorem implies that any $\mathbf{v} \in \mathbb{R}^n$ can be decomposed into its orthogonal projection onto $U$ and a vector orthogonal to it.

DEFINITION (Orthogonal Complement) $\idx{orthogonal complement}\xdi$ Let $U \subseteq \mathbb{R}^n$ be a linear subspace. The orthogonal complement of $U$, denoted $U^\perp$, is defined as

\[ U^\perp = \{\mathbf{w} \in \mathbb{R}^n\,:\, \langle \mathbf{w}, \mathbf{u}\rangle = 0, \forall \mathbf{u} \in U\}. \]

$\natural$

EXAMPLE: Continuing a previous example, we compute the orthogonal complement of the linear subspace $W = \mathrm{span}(\mathbf{w}_1,\mathbf{w}_2,\mathbf{w}_3)$, where $\mathbf{w}_1 = (1,0,1)$, $\mathbf{w}_2 = (0,1,1)$, and $\mathbf{w}_3 = (1,-1,0)$. One way to proceed is to find all vectors that are orthogonal to the orthonormal basis

\[\begin{split} \mathbf{q}_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix}, \quad \mathbf{q}_2 = \frac{1}{\sqrt{6}} \begin{pmatrix} -1\\ 2\\ 1 \end{pmatrix}. \end{split}\]

We require

\[ 0 = \langle \mathbf{u}, \mathbf{q}_1 \rangle = u_1 \left(\frac{1}{\sqrt{2}}\right) + u_2 \left(\frac{0}{\sqrt{2}}\right) + u_3 \left(\frac{1}{\sqrt{2}}\right) = \frac{u_1 + u_3}{\sqrt{2}}, \]

\[ 0= \langle \mathbf{u}, \mathbf{q}_2 \rangle = u_1 \left(-\frac{1}{\sqrt{6}}\right) + u_2 \left(\frac{2}{\sqrt{6}}\right) + u_3 \left(\frac{1}{\sqrt{6}}\right) = \frac{-u_1 + 2 u_2 + u_3}{\sqrt{6}}. \]

The first equation implies $u_3 = -u_1$, which after replacing into the second equation and rearranging gives $u_2 = u_1$.

So all vectors of the form $(u_1,u_1,-u_1)^T$ for some $u_1 \in \mathbb{R}$ are orthogonal to all of $W$. This is a one-dimensional linear subspace. We can choose an orthonormal basis by finding a solution to

\[ 1 = (u_1)^2 + (u_1)^2 + (-u_1)^2 = 3 u_1^2, \]

Take $u_1 = 1/\sqrt{3}$, that is, let

\[\begin{split} \mathbf{q}_3 = \frac{1}{\sqrt{3}} \begin{pmatrix} 1\\ 1\\ -1 \end{pmatrix}. \end{split}\]

Then we have

\[ W^\perp = \mathrm{span}(\mathbf{q}_3). \]

$\lhd$

LEMMA (Orthogonal Decomposition) $\idx{orthogonal decomposition lemma}\xdi$ Let $U \subseteq \mathbb{R}^n$ be a linear subspace and let $\mathbf{v} \in \mathbb{R}^n$. Then $\mathbf{v}$ can be decomposed as $\mathrm{proj}_U \mathbf{v} + (\mathbf{v} - \mathrm{proj}_U\mathbf{v})$ where $\mathrm{proj}_U \mathbf{v} \in U$ and $(\mathbf{v} - \mathrm{proj}_U \mathbf{v}) \in U^\perp$. Moreover, this decomposition is unique in the following sense: if $\mathbf{v} = \mathbf{u} + \mathbf{u}^\perp$ with $\mathbf{u} \in U$ and $\mathbf{u}^\perp \in U^\perp$, then $\mathbf{u} = \mathrm{proj}_U \mathbf{v}$ and $\mathbf{u}^\perp = \mathbf{v} - \mathrm{proj}_U \mathbf{v}$. $\flat$

Proof: The first part is an immediate consequence of the Orthogonal Projection Theorem. For the second part, assume $\mathbf{v} = \mathbf{u} + \mathbf{u}^\perp$ with $\mathbf{u} \in U$ and $\mathbf{u}^\perp \in U^\perp$. Subtracting $\mathbf{v} = \mathrm{proj}_U \mathbf{v} + (\mathbf{v} - \mathrm{proj}_U\mathbf{v})$, we see that

\[ (*) \qquad \mathbf{0} = \mathbf{w}_1 + \mathbf{w}_2 \]

with

\[ \mathbf{w}_1 = \mathbf{u} - \mathrm{proj}_U \mathbf{v} \in U, \qquad \mathbf{w}_2 = \mathbf{u}^\perp - (\mathbf{v} - \mathrm{proj}_U\mathbf{v}) \in U^\perp. \]

If $\mathbf{w}_1 = \mathbf{w}_2 = \mathbf{0}$, we are done. Otherwise, they must both be nonzero by $(*)$. Further, by the Properties of Orthonormal Lists, $\mathbf{w}_1$ and $\mathbf{w}_2$ must be linearly independent. But this is contradicted by the fact that $\mathbf{w}_2 = - \mathbf{w}_1$ by $(*)$. $\square$

Figure: Orthogonal decomposition (Source)

$\bowtie$

Formally, the Orthogonal Decomposition Lemma states that $\mathbb{R}^n$ is a direct sum of any linear subspace $U$ and of its orthogonal complement $U^\perp$: that is, any vector $\mathbf{v} \in \mathbb{R}^n$ can be written uniquely as $\mathbf{v} = \mathbf{u} + \mathbf{u}^\perp$ with $\mathbf{u} \in U$ and $\mathbf{u}^\perp \in U^\perp$. This is denoted $\mathbb{R}^n = U \oplus U^\perp$.

Let $\mathbf{a}_1,\ldots,\mathbf{a}_\ell$ be an orthonormal basis of $U$ and $\mathbf{b}_1,\ldots,\mathbf{b}_k$ be an orthonormal basis of $U^\perp$. By definition of the orthogonal complement, the list

\[ \mathcal{L} = \{\mathbf{a}_1,\ldots,\mathbf{a}_\ell, \mathbf{b}_1,\ldots,\mathbf{b}_k\} \]

is orthonormal, so it forms a basis of its span. Because any vector in $\mathbb{R}^n$ can be written as a sum of a vector from $U$ and a vector from $U^\perp$, all of $\mathbb{R}^n$ is in the span of $\mathcal{L}$. It follows from the Dimension Theorem that $n = \ell + k$, that is,

\[ \mathrm{dim}(U) + \mathrm{dim}(U^\perp) = n. \]

2.3.4. Overdetermined systems#

In this section, we discuss the least-squares problem. Let again $A \in \mathbb{R}^{n\times m}$ be an $n\times m$ matrix with linearly independent columns and let $\mathbf{b} \in \mathbb{R}^n$ be a vector. We are looking to solve the system

\[ A \mathbf{x} \approx \mathbf{b}. \]

If $n=m$, we can use the matrix inverse to solve the system, as discussed in the previous subsection. But we are interested in the overdetermined case, i.e. when $n > m$: there are more equations than variables. We cannot use the matrix inverse then. Indeed, because the columns do not span all of $\mathbb{R}^n$, there is a vector $\mathbf{b} \in \mathbb{R}^n$ that is not in the column space of $A$.

A natural way to make sense of the overdetermined problem is to cast it as the linear least squares problem$\idx{least squares problem}\xdi$

\[ \min_{\mathbf{x} \in \mathbb{R}^m} \|A \mathbf{x} - \mathbf{b}\|. \]

In words, we look for the best-fitting solution under the Euclidean norm. Equivalently, writing

\[\begin{split} A = \begin{pmatrix} | & & | \\ \mathbf{a}_1 & \ldots & \mathbf{a}_m \\ | & & | \end{pmatrix} = \begin{pmatrix} a_{11} & \cdots & a_{1m} \\ a_{21} & \cdots & a_{2m} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nm} \end{pmatrix} \quad \text{and} \quad \mathbf{b} = \begin{pmatrix} b_1 \\ \vdots \\ b_n \end{pmatrix} \end{split}\]

we seek a linear combination of the columns of $A$ that minimizes the objective

\[ \left\|\,\sum_{j=1}^m x_j \mathbf{a}_j - \mathbf{b}\,\right\|^2 = \sum_{i=1}^n \left( \sum_{j=1}^m a_{ij} x_j - b_i \right)^2. \]

We have already solved a closely related problem when we introduced the orthogonal projection. We make the connection explicit next.

THEOREM (Normal Equations) $\idx{normal equations}\xdi$ Let $A \in \mathbb{R}^{n\times m}$ be an $n\times m$ matrix with $n \geq m$ and let $\mathbf{b} \in \mathbb{R}^n$ be a vector. A solution $\mathbf{x}^*$ to the linear least squares problem

\[ \min_{\mathbf{x} \in \mathbb{R}^m} \|A \mathbf{x} - \mathbf{b}\| \]

satisfies the normal equations

\[ A^T A \mathbf{x}^* = A^T \mathbf{b}. \]

If further the columns of $A$ are linearly independent, then there exists a unique solution $\mathbf{x}^*$. $\sharp$

Proof idea: Apply our characterization of the orthogonal projection onto the column space of $A$.

Proof: Let $U = \mathrm{col}(A) = \mathrm{span}(\mathbf{a}_1,\ldots,\mathbf{a}_m)$. By the Orthogonal Projection Theorem, the orthogonal projection $\mathbf{p}^* = \mathrm{proj}_{U} \mathbf{b}$ of $\mathbf{b}$ onto $U$ is the unique, closest vector to $\mathbf{b}$ in $U$, that is,

\[ \mathbf{p}^* = \arg\min_{\mathbf{p} \in U} \|\mathbf{p} - \mathbf{b}\|. \]

Because $\mathbf{p}^*$ is in $U = \mathrm{col}(A)$, it must be of the form $\mathbf{p}^* = A \mathbf{x}^*$. This establishes that $\mathbf{x}^*$ is a solution to the linear least squares problem in the statement.

Important observation: while we have shown that $\mathbf{p}^*$ is unique (by the Orthogonal Projection Theorem), it is not clear at all that $\mathbf{x}^*$ (i.e., the linear combination of columns of $A$ corresponding to $\mathbf{p}^*$) is unique. By the Orthogonal Projection Theorem, it must satisfy $\langle \mathbf{b} - A \mathbf{x}^*, \mathbf{u}\rangle = 0$ for all $\mathbf{u} \in U$. Because the columns $\mathbf{a}_i$ are in $U$, that implies that

\[ 0 = \langle \mathbf{b} - A \mathbf{x}^*, \mathbf{a}_i\rangle = \mathbf{a}_i^T (\mathbf{b} - A \mathbf{x}^*) ,\qquad \forall i\in [m]. \]

Stacking up these equations gives in matrix form

\[ A^T (\mathbf{b} - A\mathbf{x}^*) = \mathbf{0}, \]

as claimed.

We have seen in a previous example that, when $A$ has full column rank, the matrix $A^T A$ is invertible. That implies the uniqueness claim. $\square$

NUMERICAL CORNER: To solve a linear system in Numpy, use numpy.linalg.solve. As an example, we consider the overdetermined system with

\[\begin{split} A = \begin{pmatrix} 1 & 0\\ 0 & 1\\ 1 & 1 \end{pmatrix} \quad \text{and} \quad \mathbf{b} = \begin{pmatrix} 0\\ 0\\ 2 \end{pmatrix}. \end{split}\]

We use numpy.ndarray.T for the transpose.

w1 = np.array([1., 0., 1.])
w2 = np.array([0., 1., 1.])
A = np.stack((w1, w2),axis=-1)
b = np.array([0., 0., 2.])
x = LA.solve(A.T @ A, A.T @ b)
print(x)

[0.66666667 0.66666667]

We can also use numpy.linalg.lstsq directly on the overdetermined system to compute the least-square solution.

x = LA.lstsq(A, b, rcond=None)[0]
print(x)

[0.66666667 0.66666667]

$\unlhd$

Self-assessment quiz (with help from Claude, Gemini, and ChatGPT)

1 Let $\mathbf{q}_1, \dots, \mathbf{q}_m$ be an orthonormal list of vectors in $\mathbb{R}^n$. Which of the following is the orthogonal projection of a vector $\mathbf{v} \in \mathbb{R}^n$ onto $\mathrm{span}(\mathbf{q}_1, \dots, \mathbf{q}_m)$?

a) $\sum_{i=1}^m \mathbf{q}_i$

b) $\sum_{i=1}^m \langle \mathbf{v}, \mathbf{q}_i \rangle$

c) $\sum_{i=1}^m \langle \mathbf{v}, \mathbf{q}_i \rangle \mathbf{q}_i$

d) $\sum_{i=1}^m \langle \mathbf{q}_i, \mathbf{q}_i \rangle \mathbf{v}$

2 According to the Normal Equations Theorem, what condition must a solution $x^*$ to the linear least squares problem satisfy?

a) $A^T Ax^* = b$

b) $A^T Ax^* = A^T b$

c) $Ax^* = A^T b$

d) $Ax^* = b$

3 Which property characterizes the orthogonal projection $\mathrm{proj}_U \mathbf{v}$ of a vector $\mathbf{v}$ onto a subspace $U$?

a) $\mathbf{v} - \mathrm{proj}_U \mathbf{v}$ is a scalar multiple of $\mathbf{v}$.

b) $\mathbf{v} - \mathrm{proj}_U \mathbf{v}$ is orthogonal to $\mathbf{v}$.

c) $\mathbf{v} - \mathrm{proj}_U \mathbf{v}$ is orthogonal to $U$.

d) $\mathrm{proj}_U \mathbf{v}$ is always the zero vector.

4 What is the interpretation of the linear least squares problem $A\mathbf{x} \approx \mathbf{b}$ in terms of the column space of $A$?

a) Finding the exact solution $\mathbf{x}$ such that $A\mathbf{x} = \mathbf{b}$.

b) Finding the vector $\mathbf{x}$ that makes the linear combination $A\mathbf{x}$ of the columns of $A$ as close as possible to $\mathbf{b}$ in Euclidean norm.

c) Finding the orthogonal projection of $\mathbf{b}$ onto the column space of $A$.

d) Finding the orthogonal complement of the column space of $A$.

5 Which matrix equation must hold true for a matrix $Q$ to be orthogonal?

a) $Q Q^T = 0$.

b) $Q Q^T = I$.

c) $Q^T Q = 0$.

d) $Q^T = Q$.

Answer for 1: c. Justification: This is the definition of the orthogonal projection onto an orthonormal list given in the text.

Answer for 2: b. Justification: The Normal Equations Theorem states that a solution $x^*$ to the linear least squares problem satisfies $A^T Ax^* = A^T b$.

Answer for 3: c. Justification: The text states that the orthogonal projection $\mathrm{proj}_U \mathbf{v}$ has the property that “the difference $\mathbf{v} - \mathrm{proj}_U \mathbf{v}$ is orthogonal to $U$.”

Answer for 4: b. Justification: The text defines the linear least squares problem as seeking a linear combination of the columns of $A$ that minimizes the distance to $\mathbf{b}$ in Euclidean norm.

Answer for 5: b. Justification: The text defines an orthogonal matrix as a square matrix $Q$ such that $Q Q^T = I$.

Geometry of least squares: the orthogonal projection

Contents

2.3. Geometry of least squares: the orthogonal projection#

2.3.1. A key concept: orthogonality#

2.3.2. Orthogonal projection#

2.3.3. Orthogonal complement#

2.3.4. Overdetermined systems#