\(\newcommand{\P}{\mathbb{P}}\) \(\newcommand{\E}{\mathbb{E}}\) \(\newcommand{\S}{\mathcal{S}}\) \(\newcommand{\indep}{\perp\!\!\!\perp}\)
\(\newcommand{\bpi}{\boldsymbol{\pi}}\)

5.7. Exercises

5.7.1. Warm-up worksheets

(with help from Claude, Gemini, and ChatGPT)

Section 5.2

E5.2.1 For the graph below, write down the set of vertices \(V\) and the set of edges \(E\).

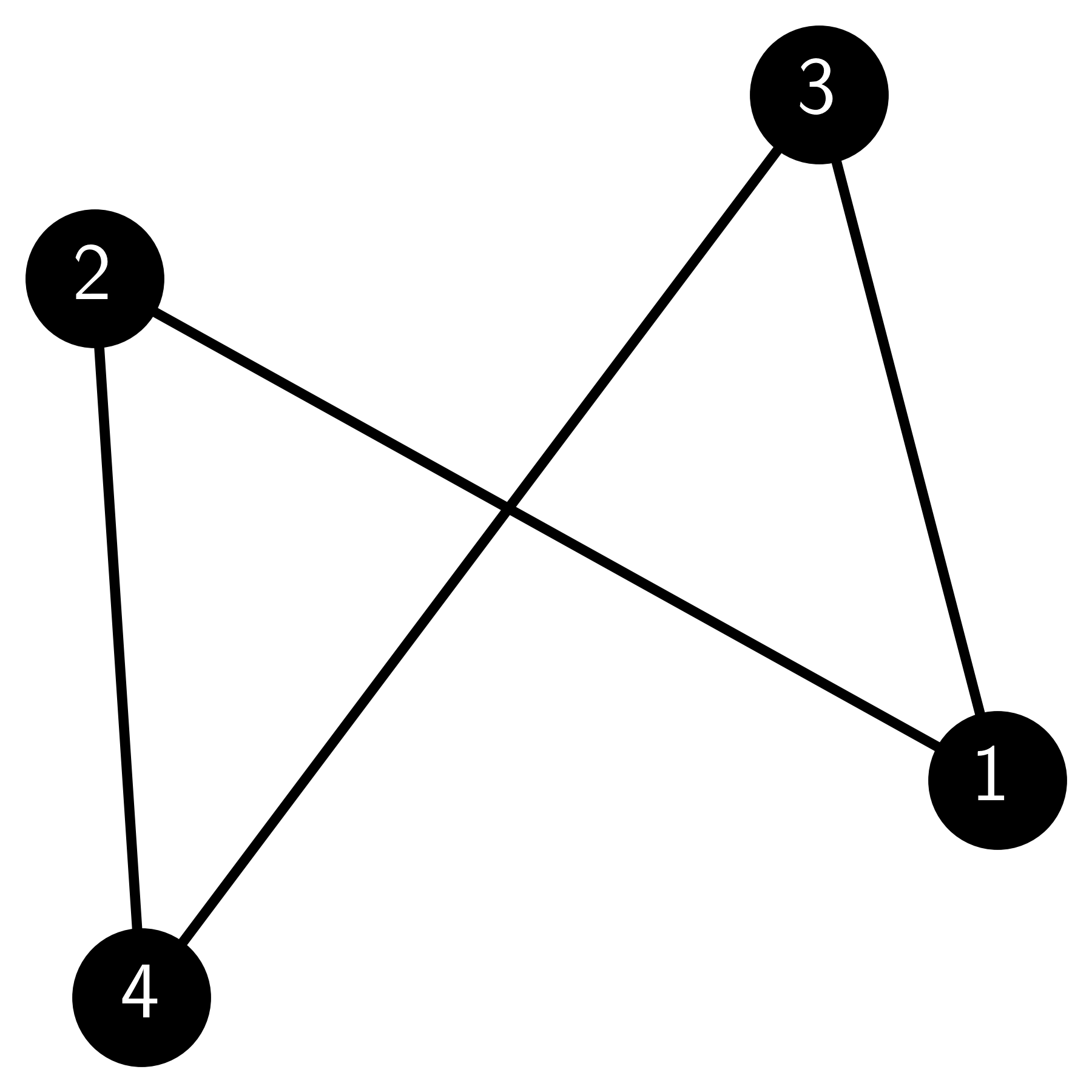
E5.2.2 For the graph in E5.2.1, write down the neighborhood \(N(1)\) and the degree \(\delta(1)\) of vertex 1.

E5.2.3 For the graph in E5.2.1, find a path between vertices 1 and 4, and compute its length.

E5.2.4 For the directed graph below, write down the adjacency matrix \(A\).

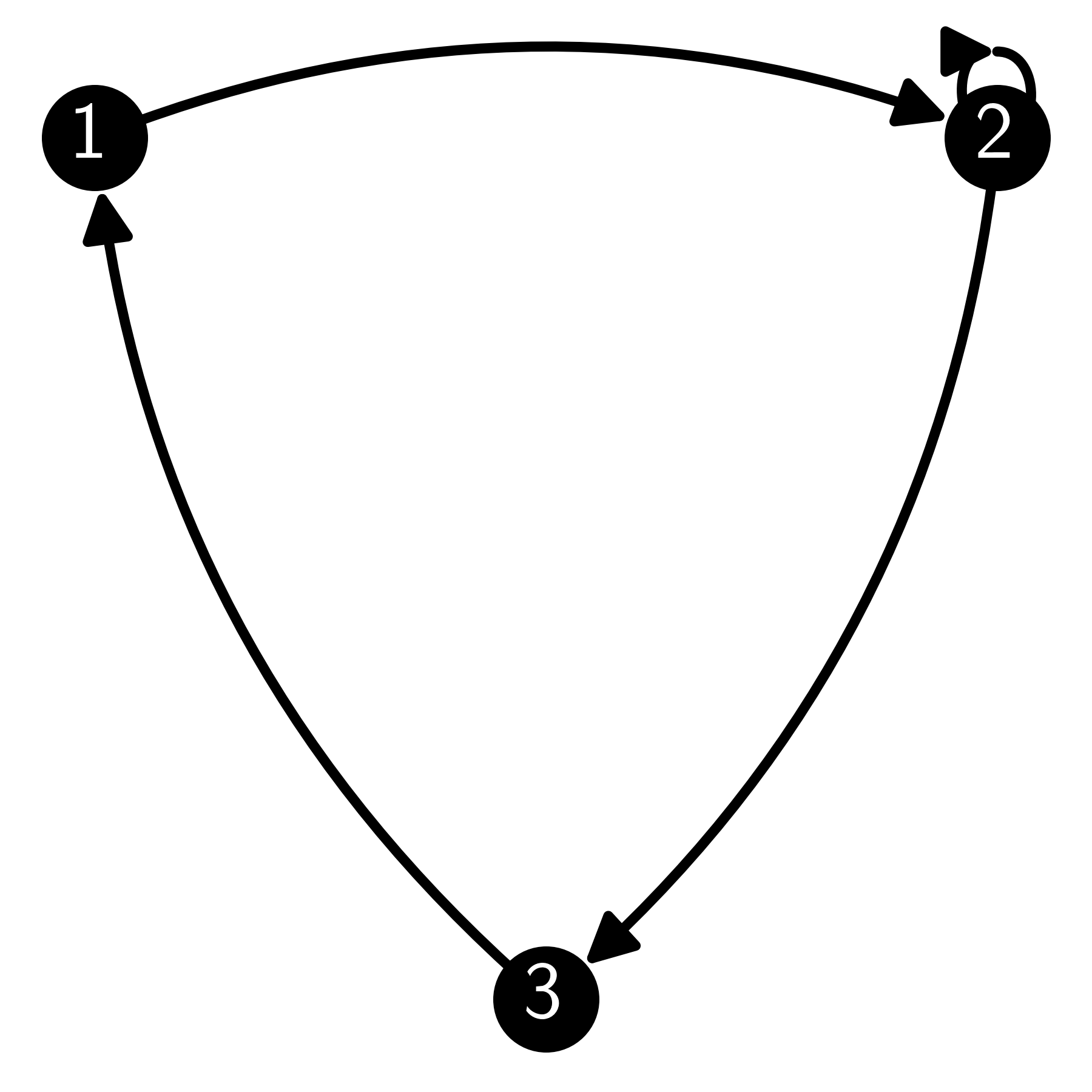
E5.2.5 For the directed graph in E5.2.4, write down the in-degree \(\delta^-(2)\) and the out-degree \(\delta^+(2)\) of vertex 2.

E5.2.6 Consider an undirected graph \(G\) with vertices \(V = \{1, 2, 3, 4\}\) and edges \(E = \{\{1, 2\}, \{2, 3\}, \{3, 4\}, \{4, 1\}\}\). Compute the degree of each vertex.

E5.2.7 Determine if the undirected graph \(G\) with vertices \(V = \{1, 2, 3, 4\}\) and edges \(E = \{\{1, 2\}, \{2, 3\}, \{3, 4\}\}\) is connected.

E5.2.8 Write the Laplacian matrix \(L\) for the undirected graph \(G\) with vertices \(V = \{1, 2, 3\}\) and edges \(E = \{\{1, 2\}, \{2, 3\}, \{1, 3\}\}\).

E5.2.9 Given an undirected graph \(G\) with vertices \(V = \{1, 2, 3, 4\}\) and edges \(E = \{\{1, 2\}, \{2, 3\}, \{3, 4\}, \{4, 1\}\}\), compute the number of connected components.

E5.2.10 Consider the following graph:

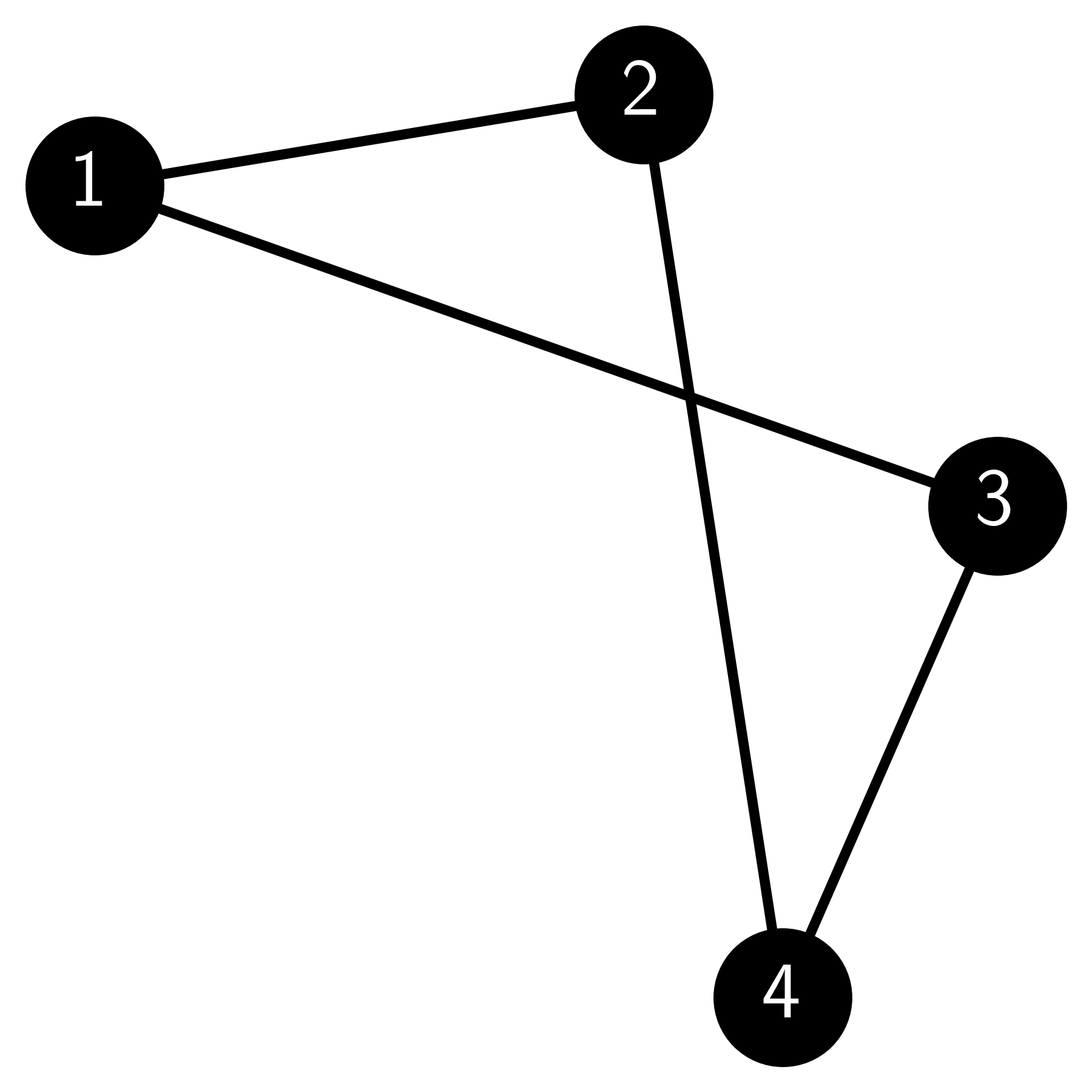
Give the adjacency matrix \(A\) of this graph.

E5.2.11 Consider the same graph as in E5.2.10. Give its incidence matrix \(B\).

E5.2.12 Consider the following directed graph:

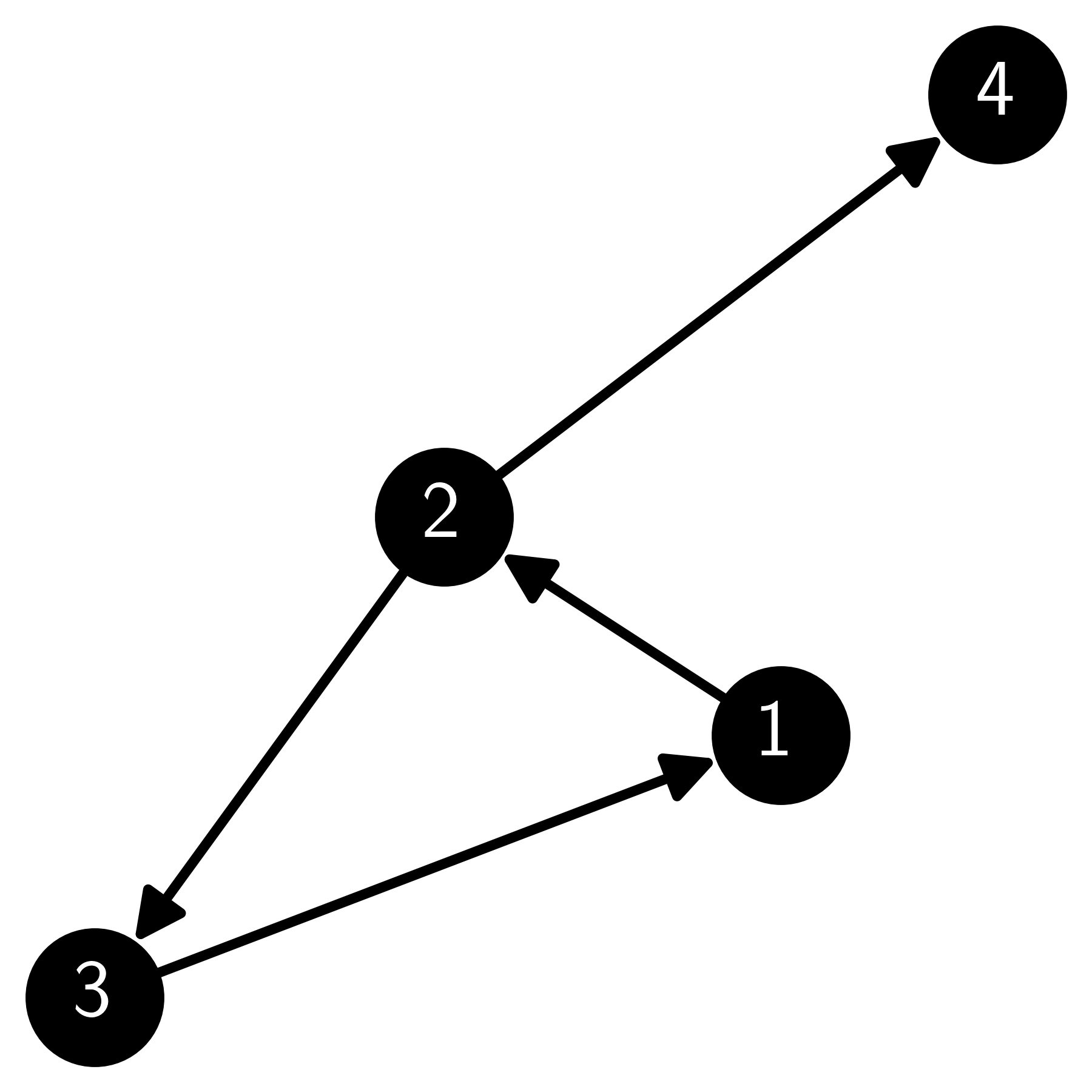
Give the adjacency matrix \(A\) of this graph.

E5.2.13 Consider the same directed graph as in E5.2.12. Give its incidence matrix \(B\).

E5.2.14 Given the directed graph \(G\) with vertices \(V = \{1, 2, 3\}\) and directed edges \(E = \{(1, 2), (2, 3), (3, 1)\}\), compute the out-degree and in-degree of each vertex.

E5.2.15 A graph is said to be \(d\)-regular if all its vertices have degree \(d\). For which value of \(d\) is the Petersen graph \(d\)-regular?

Section 5.3

E5.3.1 Let \(A = \begin{pmatrix} 5 & 3 \\ 3 & 5 \end{pmatrix}\). Find a matrix \(W\) whose columns form an orthonormal basis of \(\mathbb{R}^2\) and such that \(W^TAW\) is diagonal.

E5.3.2 Let \(A = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}\). Find the quadratic form \(\langle u, A u \rangle\) for \(u = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\).

E5.3.3 Given a symmetric matrix \(A = \begin{pmatrix} 3 & 1 \\ 1 & 2 \end{pmatrix}\) and a vector \(u = \begin{pmatrix} \frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{pmatrix}\), compute the Rayleigh quotient \(R_A(u)\).

E5.3.4 Let \(A = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}\). Compute the Rayleigh quotient \(R_A(u)\) for \(u = \begin{pmatrix} 1 \\ 1 \end{pmatrix}\).

E5.3.5 Given a symmetric matrix \(A = \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\), find the eigenvalues and eigenvectors of \(A\), and verify that the largest eigenvalue \(\lambda_1\) satisfies the variational characterization \(\lambda_1 = \max_{u \neq 0} R_A(u)\).

E5.3.6 Given a symmetric matrix \(A = \begin{pmatrix} 4 & 2 \\ 2 & 1 \end{pmatrix}\), find the eigenvalues and eigenvectors of \(A\), and verify that the smallest eigenvalue \(\lambda_2\) satisfies the variational characterization \(\lambda_2 = \min_{u \neq 0} R_A(u)\).

E5.3.7 Given a symmetric matrix \(A = \begin{pmatrix} 1 & 2 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 3 \end{pmatrix}\) and its eigenvectors \(v_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\), \(v_2 = \frac{1}{\sqrt{2}} \begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix}\), \(v_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\), verify that the second smallest eigenvalue \(\lambda_2\) satisfies the variational characterization \(\lambda_2 = \min_{0 \neq u \in V_2} R_A(u)\), where \(V_2 = \mathrm{span}(v_1, v_2)\).

E5.3.8 Let \(A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{pmatrix}\). Find the subspaces \(V_2\) and \(W_2\) as defined in the Courant-Fischer Theorem.

Section 5.4

E5.4.1 Given the graph \(G\) with adjacency matrix

\[\begin{split} A = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{pmatrix}, \end{split}\]

find the degree matrix \(D\) and the Laplacian matrix \(L\).

E5.4.2 Given the adjacency matrix of a graph \(G\) with 5 vertices

\[\begin{split} A = \begin{pmatrix} 0 & 1 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 1 & 1\\ 1 & 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 \end{pmatrix}, \end{split}\]

compute the degree matrix \(D\) and the Laplacian matrix \(L = D - A\).

E5.4.3 For the Laplacian matrix \(L\) from E5.4.2, verify that the constant unit vector \(y_1 = \frac{1}{\sqrt{5}}(1, 1, 1, 1, 1)^T\) is an eigenvector of \(L\) with eigenvalue 0.

E5.4.4 Consider the path graph \(P_4\) with 4 vertices. Draw the graph using NetworkX and compute its Laplacian matrix \(L\).

E5.4.5 For the Laplacian matrix \(L\) of \(P_4\) from E5.4.4, verify that the following vectors are eigenvectors of \(L\)

\[ y_1 = \frac{1}{2}(1, 1, 1, 1)^T, \quad y_2 = \frac{1}{2}(1, \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}, -1)^T. \]

E5.4.6 For the path graph \(P_4\), compute the Laplacian quadratic form \(y^T L y\) for the vector \(y = (1, -1, 1, -1)^T\).

E5.4.7 For the complete graph \(K_4\), find a lower and an upper bound for the largest eigenvalue \(\mu_4\) of its Laplacian matrix using the maximum degree \(\bar{\delta}\) of the graph.

E5.4.8 Consider the graph \(G\) with adjacency matrix:

\[\begin{split} A = \begin{pmatrix} 0 & 1 & 1 & 0 & 0 & 0\\ 1 & 0 & 1 & 0 & 0 & 0\\ 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 & 0 \end{pmatrix}. \end{split}\]

Find a vector \(x = (x_1, \ldots, x_6)^T\) that is an eigenvector of the Laplacian matrix of \(G\) with eigenvalue 0, such that \(x\) is not a constant vector.

E5.4.9 Let \(G\) be a graph with \(n\) vertices. Show that the sum of the entries in each row of the Laplacian matrix \(L_G\) is zero.

E5.4.10 Let \(G\) be a graph with \(n\) vertices and \(m\) edges. Compute the trace of the Laplacian matrix \(L_G\).

E5.4.11 Let \(G\) be a graph with \(n\) vertices. Show that the Laplacian matrix \(L_G\) is positive semidefinite.

E5.4.12 Let \(G\) be a graph with maximum degree \(\bar{\delta} = 3\). What is the best upper bound on the largest eigenvalue \(\mu_n\) of \(L_G\) that you can obtain from the inequality in the text?

E5.4.13 Let \(G\) be a complete graph with \(n\) vertices. Compute the eigenvalues of \(L_G\).

E5.4.14 Let \(G\) be a graph with \(n\) vertices. Show that if \(L_G\) has rank \(n-1\), then \(G\) is connected.

Section 5.5

E5.5.1 Given a graph with 5 vertices and the following adjacency matrix:

\[\begin{split} A = \begin{pmatrix} 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \end{pmatrix}, \end{split}\]

compute the cut ratio for the cut \(S = \{2\}\), \(S^c = \{1, 3, 4, 5\}\).

E5.5.2 For the graph in E5.5.1, find a cut with a smaller cut ratio than the one given in E5.5.1.

E5.5.3 For a graph with 6 vertices, what is the smallest possible value of the isoperimetric number (Cheeger constant)?

E5.5.4 Given a graph with Laplacian eigenvalues \(\mu_1 = 0\), \(\mu_2 = 0.5\), and maximum degree \(\bar{\delta} = 4\), find a lower bound for the isoperimetric number using the Cheeger Inequality.

E5.5.5 For the graph in E5.5.4, find an upper bound for the isoperimetric number using the Cheeger Inequality.

E5.5.6 Given a graph with adjacency matrix

\[\begin{split} A = \begin{pmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{pmatrix}, \end{split}\]

compute the degree matrix \(D\) and the Laplacian matrix \(L\).

E5.5.7 For the graph in E5.5.6, verify that the eigenvectors of the Laplacian matrix are \((1, 1, 1, 1)/2\), \((-1, -1, 1, 1)/2\), \((1, -1, -1, 1)/2\), and \((1, -1, 1, -1)/2\), and find their corresponding eigenvalues.

E5.5.8 Among the eigenvectors in E5.5.7, identify the Fiedler vector (the eigenvector associated with the second smallest eigenvalue of the Laplacian matrix).

E5.5.9 Using one of the Fiedler vectors from E5.5.8, order the vertices of the graph in E5.5.6 according to the graph-cutting algorithm based on the Fiedler vector.

E5.5.10 For the ordering in E5.5.9, compute the cut ratios for all possible cuts of the form \(S_k = \{\pi(1), \ldots, \pi(k)\}\), \(k \leq n-1\), and find the one with the smallest cut ratio.

E5.5.11 Find the isoperimetric number (Cheeger constant) of the graph in E5.5.6 and compare it to the results obtained in E5.5.8 and E5.5.10, as well as to the bounds given by Cheeger’s inequality.

E5.5.12 Given a graph \(G\) with vertices \(V = \{1, 2, 3, 4, 5\}\) and edges \(E = \{(1, 2), (1, 3), (2, 3), (2, 4), (3, 5)\}\), compute the adjacency matrix \(A\) of \(G\).

E5.5.13 Compute the degree matrix \(D\) for the graph \(G\) in E5.5.12.

E5.5.14 Compute the Laplacian matrix \(L\) for the graph \(G\) in E5.5.12 using \(L = D - A\).

E5.5.15 Find the cutset and cut ratio for the cut \(S = \{1, 2\}\) and \(S^c = \{3, 4, 5\}\) in the graph \(G\) from E5.5.12.

E5.5.16 Given the Fiedler vector \(y_2 \approx (0, -0.205, 0.205, -0.677, 0.677)\) corresponding to \(\mu_2 \approx 0.697\), sort the vertices based on \(y_2\) values and suggest a cut.

E5.5.17 Draw the graph \(G\) from E5.5.12 and highlight the cut \(S = \{1, 2\}\) and \(S^c = \{3, 4, 5\}\) using NetworkX in Python.

Section 5.6

E5.6.1 Consider an Erdős-Rényi (ER) random graph with \(n = 6\) vertices and edge probability \(p = 0.4\). Compute the expected number of edges in the graph.

E5.6.2 Consider an ER random graph with \(n = 8\) vertices. If the expected number of edges is 14, find the edge probability \(p\).

E5.6.3 Consider an ER random graph with \(n = 10\) vertices and edge probability \(p = 0.3\). Compute the expected triangle density, i.e., \(\mathbb{E}[|T_3|/\binom{n}{3}]\), where \(|T_3|\) is the number of triangles in the graph.

E5.6.4 Consider a stochastic blockmodel (SBM) with \(n = 6\) vertices, two blocks of equal size \(\{1,2,3\}\) and \(\{4,5,6\}\), intra-block probability \(p = 0.8\), and inter-block probability \(q = 0.2\). Write down the matrix \(M = \mathbb{E}[A]\), where \(A\) is the adjacency matrix of the graph.

E5.6.5 Consider an SBM with \(n = 8\) vertices, two blocks of equal size \(\{1,2,3,4\}\) and \(\{5,6,7,8\}\), and block probability matrix \(B = \begin{pmatrix} 0.6 & 0.3 \\ 0.3 & 0.7 \end{pmatrix}\). Write down the block assignment matrix \(Z\).

E5.6.6 Consider the SBM from E5.6.5. Compute the matrix \(M = \mathbb{E}[A]\), where \(A\) is the adjacency matrix of the graph.

E5.6.7 Compute the degree distribution of a vertex in an Erdős-Rényi random graph \(G(4, 0.5)\).

E5.6.8 In a stochastic blockmodel with \(n_1 = 3\) and \(n_2 = 3\), \(B = \begin{pmatrix} 0.5 & 0.1 \\ 0.1 & 0.6 \end{pmatrix}\), calculate the expected degree of a vertex in block 1.

E5.6.9 For an Erdős-Rényi random graph \(G(n, p)\) with \(n = 3\) and \(p = 0.5\), compute the variance of the number of edges.

E5.6.10 Consider an inhomogeneous Erdős-Rényi random graph with probability matrix

\[\begin{split} M = \begin{pmatrix} 0 & 1/2 & 1/4 \\ 1/2 & 0 & 1/3 \\ 1/4 & 1/3 & 0 \end{pmatrix}. \end{split}\]

What is the probability that the graph is a triangle?

E5.6.11 Consider a stochastic blockmodel with two blocks, \(C_1 = \{1, 2\}\) and \(C_2 = \{3, 4\}\), and connection probability matrix

\[\begin{split} B = \begin{pmatrix} 3/4 & 1/4 \\ 1/4 & 1/2 \end{pmatrix}. \end{split}\]

What is the probability that there is an edge between vertices 2 and 4?

E5.6.12 Consider a stochastic blockmodel with block assignment matrix

\[\begin{split} Z = \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} \end{split}\]

and connection probability matrix

\[\begin{split} B = \begin{pmatrix} 1/2 & 1/3 \\ 1/3 & 1/4 \end{pmatrix}. \end{split}\]

What is the expected adjacency matrix \(\mathbb{E}[A]\)?

E5.6.13 In a symmetric stochastic blockmodel (SSBM) with \(n=8\), \(p=3/4\), and \(q=1/4\), what is the expected degree of each vertex?

E5.6.14 In a symmetric stochastic blockmodel (SSBM) with \(n=12\), \(p=5/6\), \(q=1/6\), and blocks \(\{1,\ldots,6\}\) and \(\{7,\ldots,12\}\), what is the expected Laplacian matrix \(L\)?

E5.6.15 Consider an inhomogeneous Erdős-Rényi random graph with probability matrix

\[\begin{split} M = \begin{pmatrix} 0 & 1/2 & 1/4 \\ 1/2 & 0 & 1/2 \\ 1/4 & 1/2 & 0 \end{pmatrix}. \end{split}\]

What is the variance of the number of edges present in the graph?

5.7.2. Problems

5.1 Let \(A \in \mathbb{R}^{d \times d}\) be a symmetric matrix. Let \(\mathbf{v}\) be a (not necessarily unit) eigenvector of \(A\) with eigenvalue \(\lambda\). Show that \(\mathcal{R}_A(\mathbf{v}) = \lambda\). \(\lhd\)

5.2 A graph \(G = (V, E)\) is bipartite if there is a bipartition of the vertices \(V_1, V_2\) (i.e. \(V_1 \cap V_2 = \emptyset\) and \(V_1 \cup V_2 = V\)) such that all edges are between \(V_1\) and \(V_2\), that is, for any edge \(e = \{u, v\} \in E\) we have that \(e \cap V_1 \neq \emptyset\) and \(e \cap V_2 \neq \emptyset\). A graph is \(\delta\)-regular if all its vertices have degree \(\delta\). Show that if \(G\) is a \(\delta\)-regular, bipartite graph, then its adjacency matrix has an eigenvalue \(-\delta\). [Hint: Try a vector that takes different values on \(V_1\) and \(V_2\).] \(\lhd\)

5.3 In the first step of the proof of the Spectral Theorem:

a) Prove that \(\mathbf{z}\) is a unit vector.

b) Justify formally that \(\mathbf{w}_1 \neq \mathbf{0}\) implies that \(\mathbf{z}^T A_1 \mathbf{z} > \lambda_1\) for \(\delta > 0\) small enough.

\(\lhd\)

5.4 Consider the block matrices

\[\begin{split} \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix} \quad \text{and} \quad \begin{pmatrix} A & B\\ C & D \end{pmatrix} \end{split}\]

where \(\mathbf{y}\in\mathbb{R}^{d_1}\), \(\mathbf{z}\in\mathbb{R}^{d_2}\), \(A \in \mathbb{R}^{d_1 \times d_1}\), \(B \in \mathbb{R}^{d_1 \times d_2}\), \(C \in \mathbb{R}^{d_2 \times d_1}\), and \(D \in \mathbb{R}^{d_2 \times d_2}\). Show that

\[\begin{split} \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix}^T \begin{pmatrix} A & B\\ C & D \end{pmatrix} \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix} = \mathbf{y}^T A \mathbf{y} + \mathbf{y}^T B \mathbf{z} + \mathbf{z}^T C \mathbf{y} + \mathbf{z}^T D \mathbf{z}. \end{split}\]

\(\lhd\)

5.5 The trace of a square matrix \(A \in \mathbb{R}^{n \times n}\), denoted \(\mathrm{tr}(A)\), is the sum of its diagonal elements. That is,

\[ \mathrm{tr}(A) = \sum_{i=1}^n A_{ii}. \]

a) Show by direct computation that, for any two matrices \(A \in \mathbb{R}^{n \times m}, B \in \mathbb{R}^{m \times n}\),

\[ \mathrm{tr}(A B) = \mathrm{tr}(B A). \]

b) Use (a) to show that, for any three matrices \(A, B, C \in \mathbb{R}^{n \times n}\),

\[ \mathrm{tr}(A B C) = \mathrm{tr}(C A B). \]

c) Use (b) and the Spectral Theorem to show that, for any symmetric matrix \(A\), the trace of \(A\) is the sum of its eigenvalues.\(\lhd\)

5.6 Let \(A^n\) be the \(n\)-th matrix power of the adjacency matrix \(A\) of a graph \(G = (V, E)\). Prove that the \((i,j)\)-th entry \(a^n_{ij}\) is the number of paths of length exactly \(n\) between vertices \(i\) and \(j\) in \(G\). [Hint: Use induction on \(n\).] \(\lhd\)

5.7 Let \(A^n\) be the \(n\)-th matrix power of the adjacency matrix \(A\) of a graph \(G = (V, E)\).

a) What does \(\mathrm{tr}(A^n)\) count? [Hint: Use the two previous exercises.]

b) Show that

\[ |E| = \frac{1}{2} \mathrm{tr}(A^2). \]

c) Let \(T_3\) be the set of triangles (as subgraphs) in \(G\). Show that

\[ |T_3| = \frac{1}{6} \mathrm{tr}(A^3). \]

\(\lhd\)

5.8 Let \(G\) be a graph with two connected components. Show that its Laplacian \(L\) has at least two linearly independent unit eigenvectors with eigenvalue zero. [Hint: Write \(L\) as a block matrix and use that \(\mu_1 = 0\).] \(\lhd\)

5.9 Construct a graph whose adjacency matrix is not positive semidefinite. \(\lhd\)

5.10 Show that the isoperimetric number of \(G\) is equal to

\[ \phi_G = \min\left\{ \frac{|\partial S|}{|S|} \,:\, S \subseteq V, 0 < |S| \leq \frac{1}{2}|V| \right\}. \]

\(\lhd\)

5.11 Construct a symmetric matrix \(A\) whose eigenvector decomposition \(Q \Lambda Q^T\) is not unique. What is special about the eigenvalues of your example? (Hint: A small, simple matrix will do.) \(\lhd\)

5.12 Consider the following graph \(G\).

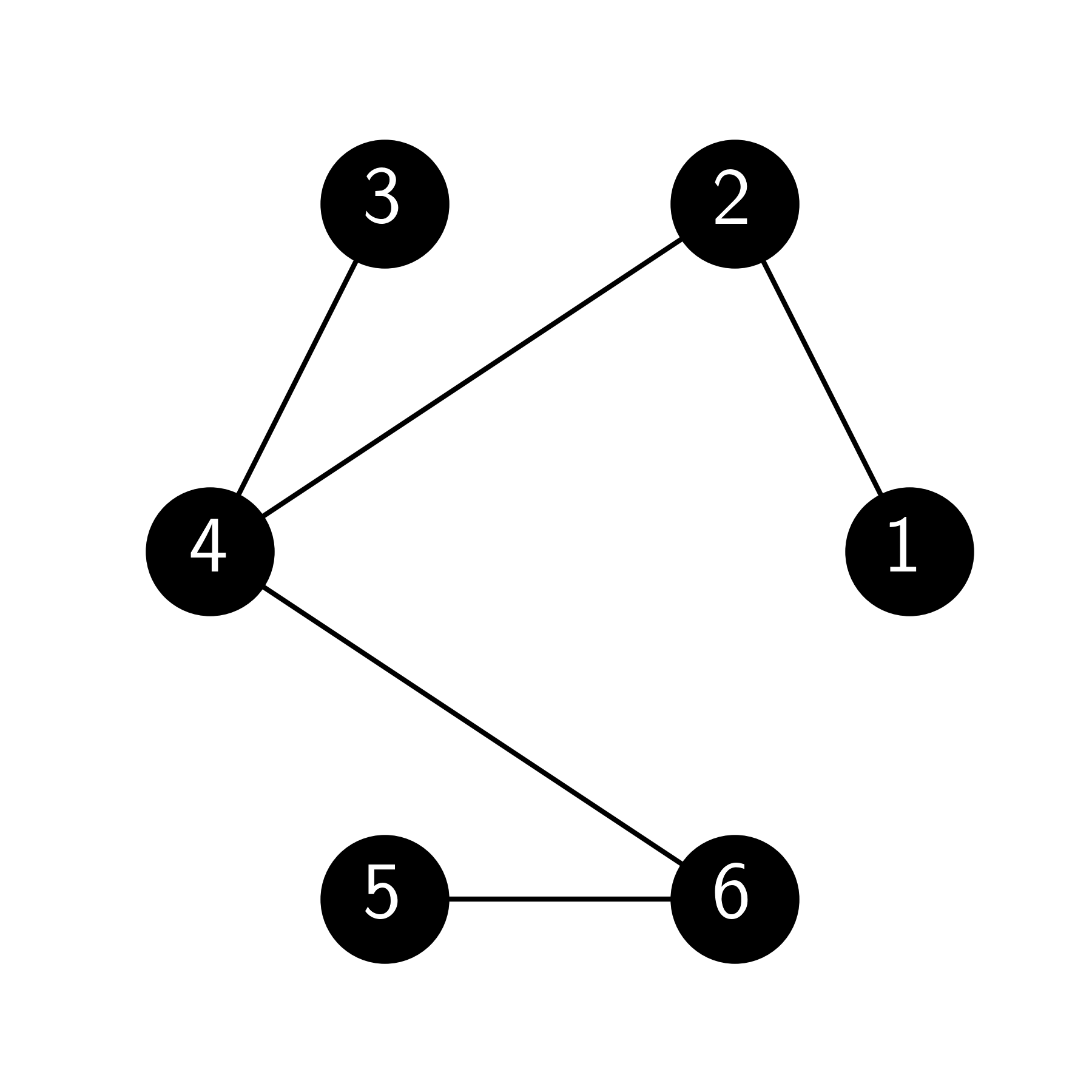
a) Compute the adjacency matrix of \(G\).

b) Compute an oriented incidence matrix of \(G\).

c) Compute the degree matrix of \(G\).

d) Compute the Laplacian matrix of \(G\).

\(\lhd\)

5.13 Prove the local formulas in the Courant-Fischer theorem. \(\lhd\)

5.14 Let \(L\) be the Laplacian matrix of a graph \(G = (V,E)\) with \(V = \{1,\ldots,n\}\). Show that for any \(\mathbf{x} \in \mathbb{R}^n\)

\[ (L \mathbf{x})_i = \sum_{j: \{i,j\} \in E} (x_i - x_j). \]

[Hint: Use the representation in terms of an oriented incidence matrix.] \(\lhd\)

5.15 Let \(G = (V,E)\) be a path graph with \(n=6\) vertices denoted \(1,\ldots,6\). That is, a graph of the following form.

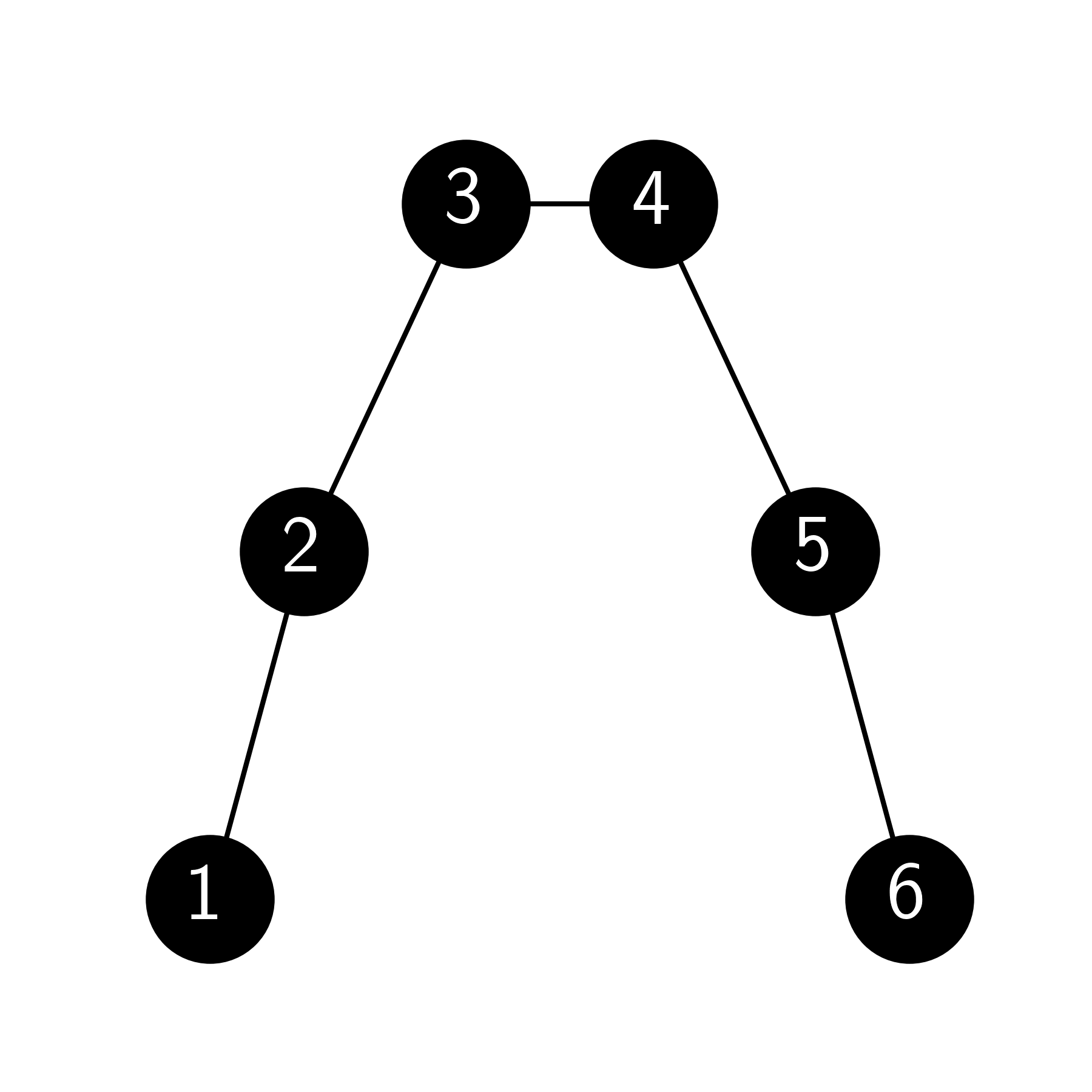
For \(\mathbf{x} \in \mathbb{R}^n\), compute \(L \mathbf{x}\). [Hint: Do Problem 5.14 first.]\(\lhd\)

5.16 Let \(G = (V,E)\) be a (3,3) grid graph. That is, a graph of the following form.

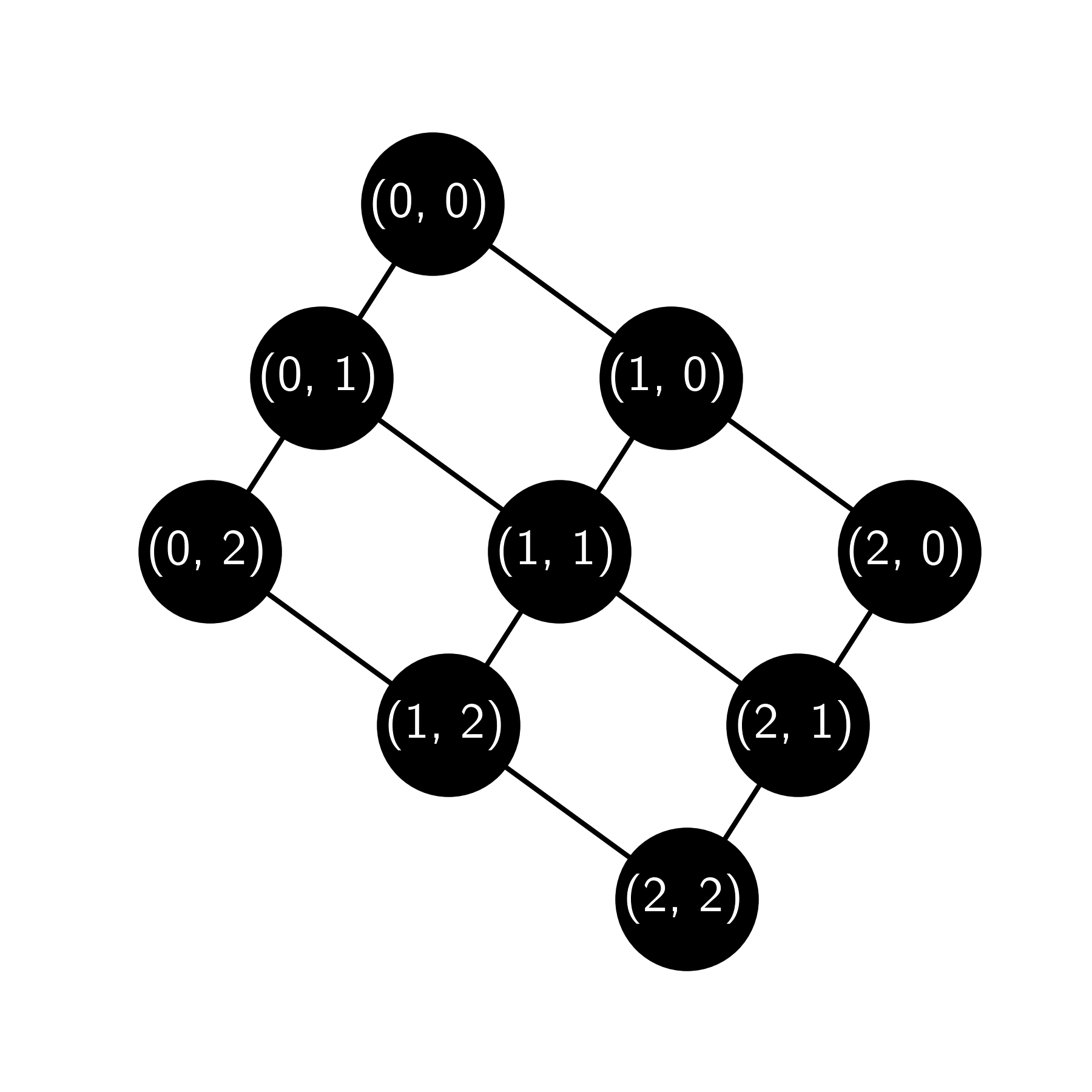
For \(\mathbf{x} \in \mathbb{R}^n\), compute \((L \mathbf{x})_v\), where \(v\) is the central vertex denoted \((1,1)\) above. [Hint: Do Problem 5.14 first.]\(\lhd\)

5.17 Let \(\mathbf{v}_1,\ldots,\mathbf{v}_d\) be an orthonormal list in \(\mathbb{R}^d\). Show that

\[ \mathrm{span}(\mathbf{v}_1,\ldots,\mathbf{v}_\ell)^\perp = \mathrm{span}(\mathbf{v}_{\ell+1},\ldots,\mathbf{v}_d) \]

for any \(\ell=1,\ldots,d\). \(\lhd\)

5.18 Let \(G = (V,E)\) be an undirected, unweighted graph. Show that

\[ \sum_{i \in V} \delta(i) = 2 |E|. \]

\(\lhd\)

5.19 Let \(G = (V,E)\) be a graph with vertices \([n]\). Recall that \(\delta(i)\) is the degree of \(i\). Let \(P_2\) be the set of paths of length \(2\) (as subgraphs) in \(G\). Show that

\[ |P_2| = \sum_{i=1}^n \binom{\delta(i)}{2}. \]

\(\lhd\)

5.20 Recall that in an Erdős-Rényi random graph \(G\) on \(n\) vertices with parameter \(p\in (0,1)\), each possible edge \(\{i,j\}\) is present (i.e., \(\{i,j\} \in E\)) with probability \(p\), independently of all other possible edges. Let \(T_3\) be the set of triangles (as subgraphs) in \(G\). Compute \(\mathrm{Var}[|T_3|]\). [Hint: Most pairs of triangles are independent, but not all of them.] \(\lhd\)

5.21 Let \(G = (V,E)\) be a graph. Let \(\emptyset \neq S \subset V\) be a proper, nonempty subset of \(V\) such that \(0 < |S| \leq \frac{1}{2}|V|\). Assume further that \(n = |V|\) is odd. Show that

\[ \phi(S) \leq |S^c|. \]

Conclude that

\[ \phi_G \leq \frac{n+1}{2}. \]

\(\lhd\)

5.22 Let \(G= (V,E)\) be a connected graph with \(V = [n]\) and Laplacian matrix \(L\). Show that

\[ \mathrm{dim}(\mathrm{null}(L)) = 1, \qquad \mathrm{dim}(\mathrm{col}(L)) = n-1. \]

\(\lhd\)

5.23 Show that

\[ \min\left\{\frac{1}{4} \sum_{\{i,j\} \in E} (x_i - x_j)^2\,:\, \mathbf{x} = (x_1,\ldots,x_n)^T \in \mathbb{R}^n, \sum_{i=1}^n x_i = 0, \sum_{i=1}^n x_i^2 = n\right\} = \frac{\mu_2 n}{4}. \]

\(\lhd\)

5.24 Let \(G = (V,E)\) be a connected graph with \(n\) vertices.

(a) Show that \(|E(S,S^c)| \geq 1\) for any cut \((S,S^c)\).

(b) Show that

\[ \phi_G \geq \frac{2}{n}. \]

\(\lhd\)

5.25 Let \(G = (V,E)\) be the \(n\)-dimensional Boolean hypercube, that is,

\[ V = \{0,1\}^n := \{\mathbf{x}= (x_1,\ldots,x_n)\,:\, x_i \in \{0,1\}, \forall i\}. \]

and

\[ E = \{\{\mathbf{x}, \mathbf{y}\}\,:\,\mathbf{x}, \mathbf{y} \in V, \|\mathbf{x} - \mathbf{y}\|_1 = 1\}, \]

where recall that \(\|\mathbf{z}\|_1 = \sum_{i=1}^n |z_i|.\) In words, the edges of \(G\) are all pairs of vectors in {0,1}^n that differ by exactly one coordinate.

a) For \(i \in \{1,\ldots,n\}\), consider the cut \((S, S^c)\) where

\[ S = \{\mathbf{x}= (x_1,\ldots,x_n) \in V\,:\, x_i = 0\}. \]

Compute \(\phi(S)\).

b) Use (a) to give an upper bound on \(\mu_2\), the second smallest eigenvalue of the Laplacian matrix of \(G\). \(\lhd\)

5.26 Let \(G = (V, E)\) be the \(n\)-cycle graph, that is, \(V = [n]\) and \(E\) contains all edges of the form \(\{i, i+1\}\) for \(i=1,\ldots,n-1\) plus the edge \(\{n,1\}\).

a) For \(k=1,\ldots,n-1\), consider the cut \((S_k,S_k^c)\) with \(S_k=\{1,\ldots,k\}\). Compute \(\phi(S_k)\). [Hint: You may want to try a concrete example with small \(n\) first.]

b) Use (a) to give an upper bound on \(\mu_2\), the second smallest eigenvalue of the Laplacian matrix of \(G\). \(\lhd\)

5.27 Prove the Inverting the Order of Eigenvalues Lemma. \(\lhd\)

5.28 Prove the Power Iteration for the Second Largest Eigenvalue Lemma. \(\lhd\)

5.29 Let \(\mathbf{v}_1,\ldots,\mathbf{v}_k \in \mathbb{R}^n\) be a list of vectors. Show that

\[ \mathrm{span}(\mathbf{v}_1,\ldots,\mathbf{v}_k)^\perp = \left\{\mathbf{z} \in \mathbb{R}^n : \langle \mathbf{z}, \mathbf{v}_i \rangle = 0, \forall i \in [k]\right\}. \]

\(\lhd\)

5.30 A weighted graph is a triple \(G = (V, E, w)\) where \((V, E)\) is a graph and \(w : E \to \mathbb{R}_+\) is a function that assigns positive real weights to the edges. We write \(w_e = w_{ij}\) for the weight of edge \(e = \{i,j\}\). The degree of a vertex \(i\) is \(\delta(i) = \sum_{j:\{i,j\} \in E} w_{ij}\) and let \(D = \mathrm{diag}(\delta(1), \ldots, \delta(n))\) be the weighted degree matrix. The adjacency matrix \(A\) of \(G\) has entries

\[\begin{align*} A_{ij} = \begin{cases} w_{ij} & \text{if $\{i,j\} \in E$}\\ 0 & \text{o.w.} \end{cases} \end{align*}\]

The weighted Laplacian matrix associated to \(G\) is defined as \(L = D - A\). Prove the formula

\[ \langle \mathbf{x}, L \mathbf{x} \rangle = \sum_{\{i,j\} \in E} w_{ij} (x_i - x_j)^2 \]

for \(\mathbf{x} = (x_1,\ldots,x_n) \in \mathbb{R}^n\). [Hint: For an orientation \(G^\sigma = (V, E^\sigma)\) of \(G\) (that is, give an arbitrary direction to each edge to turn it into a digraph), consider the matrix \(B^\sigma \in \mathbb{R}^{n \times m}\) where the column corresponding to arc \((i,j)\) has \(-\sqrt{w_{ij}}\) in row \(i\) and \(\sqrt{w_{ij}}\) in row \(j\), and every other entry is \(0\).] \(\lhd\)

5.31 Using the notation from Problem 5.30, let \(G = (V, E, w)\) be a weigthed graph with weighted Laplacian \(L\). Denote the eigenvalues of \(L\) by \(0 = \mu_1 \leq \mu_2 \leq \cdots \leq \mu_n\). Prove that

\[ \mu_2 = \min\left\{ \sum_{\{u, v\} \in E} w_{uv} (x_u - x_v)^2 \,:\, \mathbf{x} = (x_1, \ldots, x_n) \in \mathbb{R}^n, \sum_{u=1}^n x_u = 0, \sum_{u = 1}^n x_u^2 = 1 \right\}. \]

\(\lhd\)

5.32 Using the notation from Problems 5.30 and 5.31, let \(G = (V, E, w)\) be a weigthed graph with weighted Laplacian \(L\), whose eigenvalues are \(0 = \mu_1 \leq \mu_2 \leq \cdots \leq \mu_n\). Define

\[ \phi(S) = \frac{\sum_{i \in S, j \in S^c} w_{ij}}{\min\{|S|, |S^c|\}} \]

for \(\emptyset \neq S \subset V\) and let

\[ \phi_G = \min\left\{ \phi(S)\,:\, \emptyset \neq S \subset V \right\}. \]

Prove the inequality \(\mu_2 \leq 2 \phi_G\) in this weighted graph case. [Hint: Adapt the proof for the unweighted case.] \(\lhd\)

5.33 Using the notation from Problem 5.30, let \(G = (V,E,w)\) be a weighted graph with adjacency matrix \(A\) and degree matrix \(D\). The normalized Laplacian of \(G\) is defined as

\[ \mathcal{L} = I - D^{-1/2} A D^{-1/2}. \]

a) Show that

\[ \mathcal{L} = D^{-1/2} L D^{-1/2}, \]

where the weighted Laplacian \(L\) was defined in Problem 5.31.

b) Show that \(\mathcal{L}\) is symmetric, positive semidefinite.

c) Let \(0 \leq \eta_1 \leq \eta_2 \leq \cdots \leq \eta_n\) be the eigenvalues of \(\mathcal{L}\). Show that \(\eta_1 = 0\).

d) Show that

\[ \mathbf{x}^T \mathcal{L} \mathbf{x} = \sum_{\{i,j\} \in E} w_{ij} \left(\frac{x_i}{\sqrt{\delta(i)}} - \frac{x_j}{\sqrt{\delta(j)}}\right)^2, \]

for \(\mathbf{x} = (x_1,\ldots,x_n)^T \in \mathbb{R}^n\).

\(\lhd\)

5.34 Using the notation from Problems 5.30 and 5.33, let \(G = (V,E,w)\) be a weighted graph with normalized Laplacian matrix \(\mathcal{L}\), whose eigenvalues are \(0 = \eta_1 \leq \eta_2 \leq \cdots \leq \eta_n\). Show that

\[ \eta_2 = \min\left\{ \sum_{\{u, v\} \in E} w_{uv} (y_u - y_v)^2 \,:\, \mathbf{y} = (y_1, \ldots, y_n)^T \in \mathbb{R}^n, \sum_{u=1}^n \delta(u) \,y_u = 0, \sum_{u = 1}^n \delta(u) \,y_u^2 = 1 \right\}. \]

[Hint: Make the change of variables \(y_i = \frac{x_i}{\sqrt{\delta(i)}}\).]\(\lhd\)

5.35 Using the notation from Problems 5.30 and 5.33, let \(G = (V,E,w)\) be a weighted graph with normalized Laplacian matrix \(\mathcal{L} = \sum_{i=1}^n \eta_i \mathbf{z}_i \mathbf{z}_i^T\). For a subset of vertices \(S \subseteq V\), let

\[ |S|_w = \sum_{i \in S} \delta(i), \]

which we refer to as the volume of \(S\). Define

\[ \phi^N(S) = \frac{\sum_{i \in S, j \in S^c} w_{ij}}{\min\{|S|_w, |S^c|_w\}} \]

for \(\emptyset \neq S \subset V\) and let

\[ \phi^N_G = \min\left\{ \phi^N(S)\,:\, \emptyset \neq S \subset V \right\}. \]

Show that

\[ \eta_2 \leq 2 \phi^N_G. \]

[Hint: Follow the proof in the unweighted case but replace cardinality of sets with their volume.]\(\lhd\)