\(\newcommand{\bmu}{\boldsymbol{\mu}}\) \(\newcommand{\bSigma}{\boldsymbol{\Sigma}}\) \(\newcommand{\bfbeta}{\boldsymbol{\beta}}\) \(\newcommand{\bflambda}{\boldsymbol{\lambda}}\) \(\newcommand{\bgamma}{\boldsymbol{\gamma}}\) \(\newcommand{\bsigma}{{\boldsymbol{\sigma}}}\) \(\newcommand{\bpi}{\boldsymbol{\pi}}\) \(\newcommand{\btheta}{{\boldsymbol{\theta}}}\) \(\newcommand{\bphi}{\boldsymbol{\phi}}\) \(\newcommand{\balpha}{\boldsymbol{\alpha}}\) \(\newcommand{\blambda}{\boldsymbol{\lambda}}\) \(\renewcommand{\P}{\mathbb{P}}\) \(\newcommand{\E}{\mathbb{E}}\) \(\newcommand{\indep}{\perp\!\!\!\perp} \newcommand{\bx}{\mathbf{x}}\) \(\newcommand{\bp}{\mathbf{p}}\) \(\renewcommand{\bx}{\mathbf{x}}\) \(\newcommand{\bX}{\mathbf{X}}\) \(\newcommand{\by}{\mathbf{y}}\) \(\newcommand{\bY}{\mathbf{Y}}\) \(\newcommand{\bz}{\mathbf{z}}\) \(\newcommand{\bZ}{\mathbf{Z}}\) \(\newcommand{\bw}{\mathbf{w}}\) \(\newcommand{\bW}{\mathbf{W}}\) \(\newcommand{\bv}{\mathbf{v}}\) \(\newcommand{\bV}{\mathbf{V}}\) \(\newcommand{\bfg}{\mathbf{g}}\) \(\newcommand{\bfh}{\mathbf{h}}\) \(\newcommand{\horz}{\rule[.5ex]{2.5ex}{0.5pt}}\) \(\renewcommand{\S}{\mathcal{S}}\) \(\newcommand{\X}{\mathcal{X}}\) \(\newcommand{\var}{\mathrm{Var}}\) \(\newcommand{\pa}{\mathrm{pa}}\) \(\newcommand{\Z}{\mathcal{Z}}\) \(\newcommand{\bh}{\mathbf{h}}\) \(\newcommand{\bb}{\mathbf{b}}\) \(\newcommand{\bc}{\mathbf{c}}\) \(\newcommand{\cE}{\mathcal{E}}\) \(\newcommand{\cP}{\mathcal{P}}\) \(\newcommand{\bbeta}{\boldsymbol{\beta}}\) \(\newcommand{\bLambda}{\boldsymbol{\Lambda}}\) \(\newcommand{\cov}{\mathrm{Cov}}\) \(\newcommand{\bfk}{\mathbf{k}}\) \(\newcommand{\idx}[1]{}\) \(\newcommand{\xdi}{}\)

3.2. Background: review of differentiable functions of several variables

We review the differential calculus of several variables. We highlight a few key results that will play an important role: the Chain Rule and the Mean Value Theorem.

3.2.1. Gradient

Recall the definition of the gradient.

DEFINITION (Gradient) \(\idx{gradient}\xdi\) Let \(f : D \to \mathbb{R}\) where \(D \subseteq \mathbb{R}^d\) and let \(\mathbf{x}_0 \in D\) be an interior point of \(D\). Assume \(f\) is continuously differentiable at \(\mathbf{x}_0\). The (column) vector

\[ \nabla f(\mathbf{x}_0) = \left(\frac{\partial f (\mathbf{x}_0)}{\partial x_1}, \ldots, \frac{\partial f (\mathbf{x}_0)}{\partial x_d}\right) \]

is called the gradient of \(f\) at \(\mathbf{x}_0\). \(\natural\)

Note that the gradient is itself a function of \(\mathbf{x}\). In fact, unlike \(f\), it is a vector-valued function.

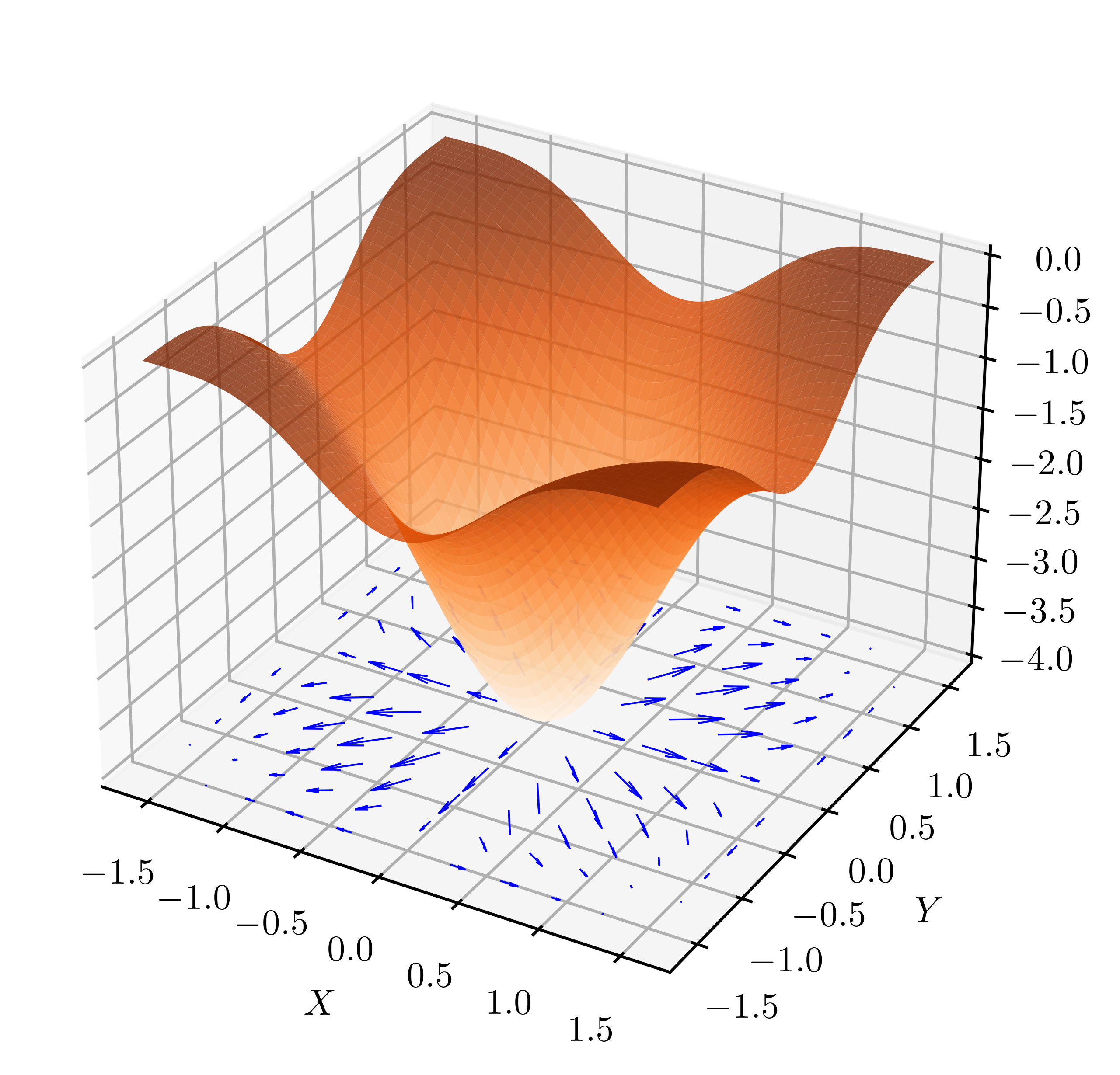
EXAMPLE: Consider the affine function

\[ f(\mathbf{x}) = \mathbf{q}^T \mathbf{x} + r \]

where \(\mathbf{x} = (x_1, \ldots, x_d)^T, \mathbf{q} = (q_1, \ldots, q_d)^T \in \mathbb{R}^d\). The partial derivatives of the linear term are given by

\[ \frac{\partial}{\partial x_i} [\mathbf{q}^T \mathbf{x}] = \frac{\partial}{\partial x_i} \left[\sum_{j=1}^d q_j x_j \right] = \frac{\partial}{\partial x_i} \left[q_i x_i \right] = q_i. \]

So the gradient of \(f\) is

\[ \nabla f(\mathbf{x}) = \mathbf{q}. \]

\(\lhd\)

EXAMPLE: Consider the quadratic function

\[ f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T P \mathbf{x} + \mathbf{q}^T \mathbf{x} + r. \]

where \(\mathbf{x} = (x_1, \ldots, x_d)^T, \mathbf{q} = (q_1, \ldots, q_d)^T \in \mathbb{R}^d\) and \(P \in \mathbb{R}^{d \times d}\). The partial derivatives of the quadratic term are given by

\[\begin{align*} \frac{\partial}{\partial x_i} [\mathbf{x}^T P \mathbf{x}] &= \frac{\partial}{\partial x_i} \left[\sum_{j, k=1}^d P_{jk} x_j x_k \right]\\ &= \frac{\partial}{\partial x_i} \left[P_{ii} x_i^2 + \sum_{j=1, j\neq i}^d P_{ji} x_j x_i + \sum_{k=1, k\neq i}^d P_{ik} x_i x_k \right], \end{align*}\]

where we used that all terms not including \(x_i\) have partial derivative \(0\).

This last expression is

\[\begin{align*} &= 2 P_{ii} x_i + \sum_{j=1, j\neq i}^d P_{ji} x_j + \sum_{k=1, k\neq i}^d P_{ik} x_k\\ &= \sum_{j=1}^d [P^T]_{ij} x_j + \sum_{k=1}^d [P]_{ik} x_k\\ &= ([P + P^T]\mathbf{x})_i. \end{align*}\]

So the gradient of \(f\) is

\[ \nabla f(\mathbf{x}) = \frac{1}{2}[P + P^T] \,\mathbf{x} + \mathbf{q}. \]

If \(P\) is symmetric, this further simplifies to \(\nabla f(\mathbf{x}) = P \,\mathbf{x} + \mathbf{q}\). \(\lhd\)

It will be useful to compute the derivative of a function \(f(\mathbf{x})\) of several variables along a parametric curve \(\mathbf{g}(t) = (g_1(t), \ldots, g_d(t))^T \in \mathbb{R}^d\) for \(t\) in some closed interval of \(\mathbb{R}\). The following result is a special case of an important fact. We will use the following notation \(\mathbf{g}'(t) = (g_1'(t), \ldots, g_m'(t))\), where \(g_i'\) is the derivative of \(g_i\). We say that \(\mathbf{g}(t)\) is continuously differentiable at \(t = t_0\) if each of its component is.

EXAMPLE: (Parametric Line) The straight line between \(\mathbf{x}_0 = (x_{0,1},\ldots,x_{0,d})^T\) and \(\mathbf{x}_1 = (x_{1,1},\ldots,x_{1,d})^T\) in \(\mathbb{R}^d\) can be parametrized as

\[ \mathbf{g}(t) = \mathbf{x}_0 + t (\mathbf{x}_1 - \mathbf{x}_0), \]

where \(t\) goes from \(0\) (at which \(\mathbf{g}(0) = \mathbf{x}_0\)) to \(1\) (at which \(\mathbf{g}(1) = \mathbf{x}_1\)).

Then

\[ g_i'(t) = \frac{\mathrm{d}}{\mathrm{d}t} [x_{0,i} + t (x_{1,i} - x_{0,i})] = x_{1,i} - x_{0,i}, \]

so that

\[ \mathbf{g}'(t) = \mathbf{x}_1 - \mathbf{x}_0. \]

\(\lhd\)

Recall the Chain Rule in the single-variable case. Quoting Wikipedia:

The simplest form of the chain rule is for real-valued functions of one real variable. It states that if \(g\) is a function that is differentiable at a point \(c\) (i.e. the derivative \(g'(c)\) exists) and f is a function that is differentiable at \(g(c)\), then the composite function \({\displaystyle f\circ g}\) is differentiable at \(c\), and the derivative is \({\displaystyle (f\circ g)'(c)=f'(g(c))\cdot g'(c)}\).

Here is a straightforward generalization of the Chain Rule.

THEOREM (Chain Rule) \(\idx{chain rule}\xdi\) Let \(f : D_1 \to \mathbb{R}\), where \(D_1 \subseteq \mathbb{R}\), and let \(g : D_2 \to \mathbb{R}\), where \(D_2 \subseteq \mathbb{R}^d\). Assume that \(f\) is continuously differentiable at \(g(\mathbf{x}_0)\), an interior point of \(D_1\), and that \(g\) is continuously differentiable at \(\mathbf{x}_0\), an interior point of \(D_2\). Then

\[ \nabla (f\circ g) (\mathbf{x}_0) = f'(g(\mathbf{x}_0)) \nabla g(\mathbf{x}_0). \]

\(\sharp\)

Proof: We apply the Chain Rule for functions of one variable to the partial derivatives. For all \(i\),

\[ \frac{\partial}{\partial x_i}f (g(\mathbf{x}_0)) = f'(g(\mathbf{x}_0)) \frac{\partial}{\partial x_i} g(\mathbf{x}_0). \]

Collecting the partial derivatives in a vector gives the claim. \(\square\)

Here is a different generalization of the Chain Rule. Again the composition \(f \circ \mathbf{g}\) denotes the function \(f \circ \mathbf{g}(t) = f (\mathbf{g}(t))\).

THEOREM (Chain Rule) Let \(f : D_1 \to \mathbb{R}\), where \(D_1 \subseteq \mathbb{R}^d\), and let \(\mathbf{g} : D_2 \to \mathbb{R}^d\), where \(D_2 \subseteq \mathbb{R}\). Assume that \(f\) is continuously differentiable at \(\mathbf{g}(t_0)\), an interior point of \(D_1\), and that \(\mathbf{g}\) is continuously differentiable at \(t_0\), an interior point of \(D_2\). Then

\[ (f\circ \mathbf{g})'(t_0) = \nabla f (\mathbf{g}(t_0))^T \mathbf{g}'(t_0). \]

\(\sharp\)

Proof: To simplify the notation, suppose that \(f\) is a real-valued function of \(\mathbf{x} = (x_1, \ldots, x_d)\) whose components are themselves functions of \(t \in \mathbb{R}\). Assume \(f\) is continuously differentiable at \(\mathbf{x}(t)\). To compute the total derivative\(\idx{total derivative}\xdi\) \(\frac{\mathrm{d} f(t)}{\mathrm{d} t}\), let \(\Delta x_k = x_k(t + \Delta t) - x_k(t)\), \(x_k = x_k(t)\) and

\[ \Delta f = f(x_1 + \Delta x_1, \ldots, x_d + \Delta x_d) - f(x_1, \ldots, x_d). \]

We seek to compute the limit \(\lim_{\Delta t \to 0} \frac{\Delta f}{\Delta t}\). To relate this limit to partial derivatives of \(f\), we re-write \(\Delta f\) as a telescoping sum where each term involves variation of a single variable \(x_k\). That is,

\[\begin{align*} \Delta f = & [f(x_1 + \Delta x_1, \ldots, x_d + \Delta x_d) - f(x_1, x_2 + \Delta x_2, \ldots, x_d + \Delta x_d)]\\ &+ [f(x_1, x_2 + \Delta x_2, \ldots, x_d + \Delta x_d) - f(x_1, x_2, x_3 + \Delta x_3, \ldots, x_d + \Delta x_d)] \\ &+ \cdots + [f(x_1, \cdots, x_{d-1}, x_d + \Delta x_d) - f(x_1, \ldots, x_d)]. \end{align*}\]

Applying the Mean Value Theorem to each term gives

\[\begin{align*} \Delta f = & \Delta x_1 \frac{\partial f(x_1 + \theta_1 \Delta x_1, x_2 + \Delta x_2, \ldots, x_d + \Delta x_d)} {\partial x_1}\\ &+ \Delta x_2 \frac{\partial f(x_1, x_2 + \theta_2 \Delta x_2, x_3 + \Delta x_3, \ldots, x_d + \Delta x_d)} {\partial x_2}\\ &+ \cdots + \Delta x_d \frac{\partial f(x_1, \cdots, x_{d-1}, x_d + \theta_d \Delta x_d)} {\partial x_d} \end{align*}\]

where \(0 < \theta_k < 1\) for \(k=1,\ldots,d\). Dividing by \(\Delta t\), taking the limit \(\Delta t \to 0\) and using the fact that \(f\) is continuously differentiable, we get

\[ \frac{\mathrm{d} f (t)}{\mathrm{d} t} = \sum_{k=1}^d \frac{\partial f(\mathbf{x}(t))} {\partial x_k} \frac{\mathrm{d} x_k(t)}{\mathrm{d} t}. \]

\(\square\)

As a first application of the Chain Rule, we generalize the Mean Value Theorem to the case of several variables. We will use this result later to prove a multivariable Taylor expansion result that will play a central role in this chapter.

THEOREM (Mean Value) \(\idx{mean value theorem}\xdi\) Let \(f : D \to \mathbb{R}\) where \(D \subseteq \mathbb{R}^d\). Let \(\mathbf{x}_0 \in D\) and \(\delta > 0\) be such that \(B_\delta(\mathbf{x}_0) \subseteq D\). If \(f\) is continuously differentiable on \(B_\delta(\mathbf{x}_0)\), then for any \(\mathbf{x} \in B_\delta(\mathbf{x}_0)\)

\[ f(\mathbf{x}) = f(\mathbf{x}_0) + \nabla f(\mathbf{x}_0 + \xi \mathbf{p})^T \mathbf{p} \]

for some \(\xi \in (0,1)\), where \(\mathbf{p} = \mathbf{x} - \mathbf{x}_0\). \(\sharp\)

One way to think of the Mean Value Theorem is as a \(0\)-th order Taylor expansion. It says that, when \(\mathbf{x}\) is close to \(\mathbf{x}_0\), the value \(f(\mathbf{x})\) is close to \(f(\mathbf{x}_0)\) in a way that can be controlled in terms of the gradient in the neighborhood of \(\mathbf{x}_0\). From this point of view, the term \(\nabla f(\mathbf{x}_0 + \xi \mathbf{p})^T \mathbf{p}\) is called the Lagrange remainder.

Proof idea: We apply the single-variable result and the Chain Rule.

Proof: Let \(\phi(t) = f(\boldsymbol{\alpha}(t))\) where \(\boldsymbol{\alpha}(t) = \mathbf{x}_0 + t \mathbf{p}\). Observe that \(\phi(0) = f(\mathbf{x}_0)\) and \(\phi(1) = f(\mathbf{x})\). By the Chain Rule and the parametric line example,

\[ \phi'(t) = \nabla f(\boldsymbol{\alpha}(t))^T \boldsymbol{\alpha}'(t) = \nabla f(\boldsymbol{\alpha}(t))^T \mathbf{p} = \nabla f(\mathbf{x}_0 + t \mathbf{p})^T \mathbf{p}. \]

In particular, \(\phi\) has a continuous first derivative on \([0,1]\). By the Mean Value Theorem in the single-variable case

\[ \phi(t) = \phi(0) + t \phi'(\xi) \]

for some \(\xi \in (0,t)\). Plugging in the expressions for \(\phi(0)\) and \(\phi'(\xi)\) and taking \(t=1\) gives the claim. \(\square\)

3.2.2. Second-order derivatives

One can also define higher-order derivatives. We start with the single-variable case, where \(f : D \to \mathbb{R}\) with \(D \subseteq \mathbb{R}\) and \(x_0 \in D\) is an interior point of \(D\). Note that, if \(f'\) exists in \(D\), then it is itself a function of \(x\). Then the second derivative at \(x_0\) is

\[ f''(x_0) = \frac{\mathrm{d}^2 f(x_0)}{\mathrm{d} x^2} = \lim_{h \to 0} \frac{f'(x_0 + h) - f'(x_0)}{h} \]

provided the limit exists.

In the several variable case, we have the following:

DEFINITION (Second Partial Derivatives and Hessian) \(\idx{second partial derivatives}\xdi\) \(\idx{Hessian}\xdi\) Let \(f : D \to \mathbb{R}\) where \(D \subseteq \mathbb{R}^d\) and let \(\mathbf{x}_0 \in D\) be an interior point of \(D\). Assume that \(f\) is continuously differentiable in an open ball around \(\mathbf{x}_0\). Then \(\partial f(\mathbf{x})/\partial x_i\) is itself a function of \(\mathbf{x}\) and its partial derivative with respect to \(x_j\), if it exists, is denoted by

\[ \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_j \partial x_i} = \lim_{h \to 0} \frac{\frac{\partial f}{\partial x_i}(\mathbf{x}_0 + h \mathbf{e}_j) - \frac{\partial f}{\partial x_i}(\mathbf{x}_0)}{h}. \]

To simplify the notation, we write this as \(\partial^2 f(\mathbf{x}_0)/\partial x_i^2\) when \(j = i\). If \(\partial^2 f(\mathbf{x})/\partial x_j \partial x_i\) and \(\partial^2 f(\mathbf{x})/\partial x_i^2\) exist and are continuous in an open ball around \(\mathbf{x}_0\) for all \(i, j\), we say that \(f\) is twice continuously differentiable at \(\mathbf{x}_0\).

The matrix of second derivatives is called the Hessian and is denoted by

\[\begin{split} \mathbf{H}_f(\mathbf{x}_0) = \begin{pmatrix} \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_1^2} & \cdots & \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_d \partial x_1}\\ \vdots & \ddots & \vdots\\ \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_1 \partial x_d} & \cdots & \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_d^2} \end{pmatrix}. \end{split}\]

\(\natural\)

Like \(f\) and the gradient \(\nabla f\), the Hessian \(\mathbf{H}_f\) is a function of \(\mathbf{x}\). It is a matrix-valued function however.

When \(f\) is twice continuously differentiable at \(\mathbf{x}_0\), its Hessian is a symmetric matrix.

THEOREM (Symmetry of the Hessian) \(\idx{symmetry of the Hessian}\xdi\) Let \(f : D \to \mathbb{R}\) where \(D \subseteq \mathbb{R}^d\) and let \(\mathbf{x}_0 \in D\) be an interior point of \(D\). Assume that \(f\) is twice continuously differentiable at \(\mathbf{x}_0\). Then for all \(i \neq j\)

\[ \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_j \partial x_i} = \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_i \partial x_j}. \]

\(\sharp\)

Proof idea: Two applications of the Mean Value Theorem show that the limits can be interchanged.

Proof: By definition of the partial derivative,

\[\begin{align*} \frac{\partial^2 f(\mathbf{x}_0)}{\partial x_j \partial x_i} &= \lim_{h_j \to 0} \frac{\frac{\partial f}{\partial x_i}(\mathbf{x}_0 + h_j \mathbf{e}_j) - \frac{\partial f}{\partial x_i}(\mathbf{x}_0)}{h_j}\\ &= \lim_{h_j \to 0} \lim_{h_i \to 0} \frac{1}{h_j h_i} \left\{ [f(\mathbf{x}_0 + h_j \mathbf{e}_j + h_i \mathbf{e}_i) - f(\mathbf{x}_0 + h_j \mathbf{e}_j)] - [f(\mathbf{x}_0 + h_i \mathbf{e}_i) - f(\mathbf{x}_0)] \right\}\\ &= \lim_{h_j \to 0} \lim_{h_i \to 0} \frac{1}{h_i} \left\{ \frac{[f(\mathbf{x}_0 + h_i \mathbf{e}_i + h_j \mathbf{e}_j) - f(\mathbf{x}_0 + h_i \mathbf{e}_i)] - [f(\mathbf{x}_0 + h_j \mathbf{e}_j) - f(\mathbf{x}_0)]}{h_j} \right\}\\ &= \lim_{h_j \to 0} \lim_{h_i \to 0} \frac{1}{h_i} \left\{\frac{\partial}{\partial x_j}[f(\mathbf{x}_0 + h_i \mathbf{e}_i + \theta_j h_j \mathbf{e}_j) - f(\mathbf{x}_0 + \theta_j h_j \mathbf{e}_j)] \right\}\\ &= \lim_{h_j \to 0} \lim_{h_i \to 0} \frac{1}{h_i} \left\{\frac{\partial f}{\partial x_j}(\mathbf{x}_0 + h_i \mathbf{e}_i + \theta_j h_j \mathbf{e}_j) - \frac{\partial f}{\partial x_j}(\mathbf{x}_0 + \theta_j h_j \mathbf{e}_j) \right\} \end{align*}\]

for some \(\theta_j \in (0,1)\). Note that, on the third line, we rearranged the terms and, on the fourth line, we applied the Mean Value Theorem to \(f(\mathbf{x}_0 + h_i \mathbf{e}_i + h_j \mathbf{e}_j) - f(\mathbf{x}_0 + h_j \mathbf{e}_j)\) as a continuously differentiable function of \(h_j\).

Because \(\partial f/\partial x_j\) is continuously differentiable in an open ball around \(\mathbf{x}_0\), a second application of the Mean Value Theorem gives for some \(\theta_i \in (0,1)\)

\[\begin{align*} &\lim_{h_j \to 0} \lim_{h_i \to 0} \frac{1}{h_i} \left\{\frac{\partial f}{\partial x_j}(\mathbf{x}_0 + h_i \mathbf{e}_i + \theta_j h_j \mathbf{e}_j) - \frac{\partial f}{\partial x_j}(\mathbf{x}_0 + \theta_j h_j \mathbf{e}_j) \right\}\\ &= \lim_{h_j \to 0} \lim_{h_i \to 0} \frac{\partial}{\partial x_i}\left[\frac{\partial f}{\partial x_j}(\mathbf{x}_0 + \theta_j h_j \mathbf{e}_j + \theta_i h_i \mathbf{e}_i)\right]\\ &= \lim_{h_j \to 0} \lim_{h_i \to 0} \frac{\partial^2 f(\mathbf{x}_0 + \theta_j h_j \mathbf{e}_j + \theta_i h_i \mathbf{e}_i)}{\partial x_i \partial x_j}. \end{align*}\]

The claim then follows from the continuity of \(\partial^2 f/\partial x_i \partial x_j\). \(\square\)

EXAMPLE: Consider the quadratic function

\[ f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T P \mathbf{x} + \mathbf{q}^T \mathbf{x} + r. \]

Recall that the gradient of \(f\) is

\[ \nabla f(\mathbf{x}) = \frac{1}{2}[P + P^T] \,\mathbf{x} + \mathbf{q}. \]

To simplify the calculation, let \(B = \frac{1}{2}[P + P^T]\) and denote the rows of \(B\) by \(\mathbf{b}_1^T, \ldots,\mathbf{b}_d^T\).

Each component of \(\nabla f\) is an affine function of \(\mathbf{x}\), specifically,

\[ \frac{\partial f (\mathbf{x})}{\partial x_i} = \mathbf{b}_i^T \mathbf{x} + q_i. \]

Row \(i\) of the Hessian is simply the gradient transposed of \(\frac{\partial f (\mathbf{x})}{\partial x_i}\) which, by our previous results, is

\[ \left(\nabla \frac{\partial f (\mathbf{x})}{\partial x_i}\right)^T = \mathbf{b}_i^T. \]

Putting this together we get

\[ \mathbf{H}_f(\mathbf{x}) = \frac{1}{2}[P + P^T]. \]

Observe that this is indeed a symmetric matrix. \(\lhd\)

Self-assessment quiz (with help from Claude, Gemini, and ChatGPT)

1 What does it mean for a function \(f\) to be continuously differentiable at \(x_0\)?

a) \(f\) is continuous at \(x_0\).

b) All partial derivatives of \(f\) exist at \(x_0\).

c) All partial derivatives of \(f\) exist and are continuous in an open ball around \(x_0\).

d) The gradient of \(f\) is zero at \(x_0\).

2 What is the gradient of a function \(f : D \to \mathbb{R}\), where \(D \subseteq \mathbb{R}^d\), at a point \(x_0 \in D\)?

a) The rate of change of \(f\) with respect to \(x\) at \(x_0\)

b) The vector of all second partial derivatives of \(f\) at \(x_0\)

c) The vector of all first partial derivatives of \(f\) at \(x_0\)

d) The matrix of all second partial derivatives of \(f\) at \(x_0\)

3 Which of the following statements is true about the Hessian matrix of a twice continuously differentiable function?

a) It is always a diagonal matrix.

b) It is always a symmetric matrix.

c) It is always an invertible matrix.

d) It is always a positive definite matrix.

4 Let \(f(x, y, z) = x^2 + y^2 - z^2\). What is the Hessian matrix of \(f\)?

a) \(\begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & -2 \end{pmatrix}\)

b) \(\begin{pmatrix} 2x & 2y & -2z \end{pmatrix}\)

c) \(\begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}\)

d) \(\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}\)

5 What is the Hessian matrix of the quadratic function \(f(x) = \frac{1}{2}x^TPx + q^Tx + r\), where \(P \in \mathbb{R}^{d \times d}\) and \(q \in \mathbb{R}^d\)?

a) \(H_f(x) = P\)

b) \(H_f(x) = P^T\)

c) \(H_f(x) = \frac{1}{2}[P + P^T]\)

d) \(H_f(x) = [P + P^T]\)

Answer for 1: c. Justification: The text states, “If \(f\) exists and is continuous in an open ball around \(x_0\) for all \(i\), then we say that \(f\) is continuously differentiable at \(x_0\).”

Answer for 2: c. Justification: From the text: “The (column) vector \(\nabla f(x_0) = ( \frac{\partial f(x_0)}{\partial x_1}, \ldots, \frac{\partial f(x_0)}{\partial x_d})\) is called the gradient of \(f\) at \(x_0\).”

Answer for 3: b). Justification: The text states: “When \(f\) is twice continuously differentiable at \(x_0\), its Hessian is a symmetric matrix.”

Answer for 4: a). Justification: The Hessian is the matrix of second partial derivatives:

\[\begin{split} \begin{pmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial x \partial z} \\ \frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial^2 f}{\partial y \partial z} \\ \frac{\partial^2 f}{\partial z \partial x} & \frac{\partial^2 f}{\partial z \partial y} & \frac{\partial^2 f}{\partial z^2} \end{pmatrix} = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & -2 \end{pmatrix} \end{split}\]

Answer for 5: c. Justification: The text shows that the Hessian of the quadratic function is \(H_f(x) = \frac{1}{2}[P + P^T]\).